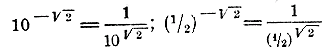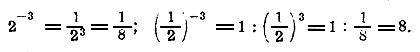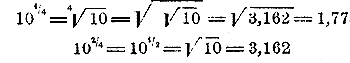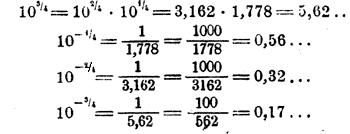| АЛГЕБРА В НАЧАЛО |
|
ОТДЕЛ ОДИННАДЦАТЫЙ. ОБОБЩЕНИЕ ПОНЯТИЯ О ПОКАЗАТЕЛЯХ. Глава первая. Целые показатели. Глава первая. Целые показатели. 255. Свойства целых положительных показателей. Показатели степени до сего времени предполагались нами целыми и положительными, причем мы им придавали смысл, выражаемый в следующем определении: Возвысить число а в степень с целым и положительным показателем n — значит найти произведение n одинаковых сомножителей ааа...a. Перечислим свойства этих показателей, известные нам из предыдущих глав алгебры: 1) при умножении степеней одного и того же числа показатели их складываются (Отдел 2 глава 3 § 53); 2) при делении степеней одного и того же числа показатель делителя вычитается из показателя делимого, если показатель делителя не больше показателя делимого (Отдел 2 глава 4 § 64); 3) всякое число, возвышенное в нулевую степень, дает 1 (Отдел 2 глава 4 § 65); 4) от возвышения отрицательного числа в степень с четным показателем получается положительное число, а с нечетным показателем— отрицательное (Отдел 6 глава 1§ 153); 5) чтобы возвысить в степень произведение, достаточно возвысить в эту степень каждый сомножитель отдельно (Отдел 6 глава 1§ 154, а); 6) чтобы возвысить степень в степень, достаточно перемножить показатели этих степеней (Отдел 6 глава 1§ 154,6); 7) чтобы возвысить в степепь дробь, достаточно возвысить в эту степень отдельно числитель и знаменатель (Отдел 6 глава 1§ 154, в); 8) чтобы возвысить радикал в степень, достаточно возвысить в эту степень подкоренное число (Отдел 8 глава 4§ 205, г); 9) чтобы извлечь корень из степени, достаточно разделить показатель степени на показатель корня, если такое деление выполняется нацело (Отдел 6 глава 4§ 168,6). Теперь мы расширим понятие о показателях, введя показатели отрицательные и дробные, которые до сего времени мы не употребляли. Мы увидим при этом, что все свойства целых положительных показателей сохраняются и для показателей отрицательных и дробных. 256. Отрицательные целые показатели. Мы видели (Отдел 2 глава 4 § 64), что при делении степеней одного и того же числа показатель делителя вычитается из показателя делимого в том случае, если показатель делителя не больше показателя делимого. Теперь мы условимся производить вычитание показателей и в том случае, когда показатель делителя больше показателя делимого; тогда мы получим в частном букву с отрицательным показателем; например: а2 : а5 = а—3. Таким образом, число с отрицательным показателем мы условимся употреблять для обозначения частного от деления степеней этого числа в том случае, когда показатель делителя превосходит показатель делимого на столько единиц, сколько их находится в абсолютной величине отрицательного показателя. Так, а—2 означает частное а : а3, или а2 : а4, или а3 : а5, вообще частное аm : аm+2. Понимаемое в этом смысле число с отрицательным показателем равно дроби, у которой числитель есть 1, а знаменатель — то же число, но с положительным показателем, равным по абсолютной величине отрицательному показателю. Действительно, согласно нашему условию, мы должны иметь:
Сократив две первые дроби на аm и третью дробь на xm (т. е. в обоих случаях сократив дроби на числитель), получим:
Заметим, что отрицательные показатели дают возможность представить всякое дробное алгебраическое выражение под видом целого; для этого стоит только все множители знаменателя перенести множителями в числитель, взяв их с отрицательными показателями. Например:
Само собою разумеется, что такое преобразование данного выражения в целое есть только изменение одного внешнего вида выражения, а не содержания его. 257. Действия над степенями с отрицательными показателями. Убедимся теперь, что все действия над степенями с отрицательными показателями можно производить по тем же правилам, какие были прежде выведены для показателей положительных. Достаточно обнаружить это только для умножения и возвышения в степень, так как правила обратных действий — деления и извлечения корня — составляют простое следствие правил прямых действий — умножения и возвышения. Умножение. Предстоит показать, что при умножении степеней показатели одинаковых букв складываются и в том случае, когда эти показатели отрицательные. Например, убедимся, что: a—2 • a—3 = a—2 +(—3) = a—5 Действительно, заменив степени с отрицательными показателями дробями и произведя действие умножения по правилам, относящимся к дробям, получим:
Подобно этому: x—4 • x3 = x—4 + 3 = x—1 так как
Возвышение в степень. Надо показать, что при возвышении в степень показатели этих степеней перемножаются и в том случае, когда они отрицательные. Например, убедимся, чтo (a—3) — 4 = a (—3) • (— 4) = a12 Действительно:
Подобно этому: (x3) — 4 = a—12 потому что
Примеры.
Дробные показатели. 258. В каком смысле употребляются дробные показатели. Мы видели (Отдел 6 глава 4§ 168,6), что при извлечении корня из степени делят показатель степени на показатель корня, если такое деление выполнется нацело; например: √a4 = a2, 3√x9 = x3 и т. п. Условимся теперь распространить это правило и на те случаи, когда показатель степени не делится нацело на показатель корня. Например, мы условимся принимать, что
Вообще мы условимся, что выражение Условимся еще допускать и отрицательные дробные показатели в том же смысле, в каком мы допустили отрицательные целые показатели; например, условимся, что
Замечание. Дробные показатели были введены в алгебру главным образом голландским инженером Симоном Стевином в начале XVII столетия Позднее, в конце XVII столетия, Оксфордский профессор Джон Валлис ввел в употребление отрицательные показатели. 259. Основное свойство дробного показателя. Величина степени с дробным показателем не изменится, если мы умножим или разделим на одно и то же число (отличное от нуля) числитель и знаменатель дробного показателя. Так:
Действительно, знаменатель дробного показателя означает показатель корня, а числитель его означает показатель подкоренного выражения, а такие показатели, как мы видели (Отдел 8 глава 4 § 202), можно умножать и делить на одно и то же число. Основываясь на этом свойстве, мы можем преобразовывать дробный показатель совершенно так же, как и обыкновенную дробь: например, мы можем сокращать дробный показатель, или приводить несколько дробных показателей к одному знаменателю. 260. Действия над степенями с дробными показателями. Предстоит показать, что к дробным показателям применимы правила, выведенные раньше для целых показателей. Это достаточно обнаружить только для умножения и возвышения в степень, так как правила деления и извлечения корня составляют следствие правил умножения и возвышения в степень. Умножение. Докажем, что при умножении показатели степеней одинаковых букв складываются и тогда, когда эти показатели дробные. Например, убедимся, что
Для этого изобразим степени с дробными показателями в виде радикалов и произведем умножение по правилу умножения радикалов (Отдел 8 глава 4 § 205,6):
Результат получился тот самый, какой мы получили после сложения показателей; значит, правило о сложении показателей (при умножении) можно применять и для дробных показателей. Таким образом:
Возвышение в степень. Докажем, что при возвышении степени в степень показатели этих степеней можно перемножить и тогда, когда эти показатели дробные. Напр., убедимся, что
Действительно, заменив радикалами степени с дробными показателями, получим:
Если показатели не только дробные числа, но и отрицательные, то и тогда к ним можно применять правила, доказанные раньше для положительных показателей. Напр.:
261. Примеры на действия с дробными и отрицательными показателями.
Некоторые свойства степени с рациональным показателем. 262. Допустим, что в степени ах основание а есть какое-нибудь положительное число, большее или меньшее 1, а показатель х любое рациональное число, положительное или отрицательное, целое или дробное. Кроме того предположим, что когда х есть какая-нибудь дробь, напр., 3/2, т. е. когда степень ах представляет собою радикал √a3, то из возможных значений этого радикала мы берем только одно арифметическое, т. е. положительное. При этих условиях степень ах обладает следующими свойствами: а) При всяком значении рационального показателя х степень ах есть число положительное. Действительно, если х есть целое положительное число, напр. 3, то ах представляет собой произведение ааа положительных чисел, и потому оно положительно. Если х есть положительная дробь, напр. 3/2, то ах означает √a3 , а мы условились из всех значений радикала брать только положительное. Если х есть отрицательное число, напр.— 3/4, то
и потому ах > 0, так как Наконец, если x = 0 , то ах =а0 = 1, т. е. тоже есть число положительное. б) Если a >1, то при положительных значениях х степень ах больше 1, а при отрицательных — меньше 1. Если же а < 1, то, наоборот, ах < 1 при х >0 и ах >1 при х< 0. Действительно, если х есть целое положительное число,напр. 3, то тогда ах = а3 = ааа. Очевидно, что если а >1, то ааа > 1, а если а < 1, то ааа < 1.
в) При возрастании показателя х степень ах возрастает, если а > 1, и убывает, если а < 1. Пусть х имеет какое-нибудь определенное значение, напр. х = 3. Тогда степень ах будет равна а3. Увеличим теперь х на какое-нибудь число, напр., вместо 3 возьмем 3,01. Тогда вместо а3 будем иметь а3,01 . Чтобы узнать, какое из этих двух чисел больше, возьмем разность а3,01 — а3 и посмотрим, при каких условиях эта разность будет положительное число и при каких отрицательное. Разность эту можно представить так: а3,01 — а3 = а3 ( а0,01 — 1) Согласно свойству (а) число а3 > 0; согласно свойству (б) число а0,01 > 1 при а >1 г) Если х стремится к ∞, то при а >1 степень ах стремится также к ∞, а при а < 1 она стремится к 0. Согласно свойству (в) при увеличении х степень ах увеличивается, если а >1, и уменьшается, если а<1. Теперь мы покажем, что, увеличиваясь при а >1, число ах может сделаться больше всякого числа, как бы велико оно ни было, а уменьшаясь при «<1, оно может сделаться меньше всякого положительного числа, как бы мало оно ни было. Для этого примем во внимание, что показатель х, увеличиваясь неограниченно, проходит, между прочим, через ряд целых значений: 1, 2, 3, 4,... Тогда степень ах будет проходить через ряд таких значений: а1 , а2, а3, а4,... Ряд этот есть бесконечная Г. П. со знаменателем а. Если a >1, то эта прогрессия возрастающая, а если a < 1, то она убывающая. Как мы видели (Отдел 10 глава 3 § 251,6), в первом случае член прогрессии, удаляясь от начала ряда, может превзойти всякое число, как бы велико оно ни было: а во втором случае член прогрессии может сделаться меньше всякого положительного числа, как бы мало оно ни было. Значит, когда х стремится к ∞, то степень ах тоже стремится к ∞, когда а > 1, и степень ах стремится к 0, когда а <1. Таким образом, мы можем написать: а∞ = ∞, если а >1; а∞ = 0, если а <1. д) Если х стремится к — ∞, то степень ах стремится к 0 при а > 1 и к ∞ при а <1. Показатель х, уменьшаясь неограниченно, проходит, между прочим, ряд целых отрицательных значений:—1,—2,—3,—4,... Тогда степень ах проходит ряд таких значении: а—1 , а—2, а—3, а— 4,... т. е.
Этот ряд есть бесконечная Г. П. со знаменателем 1/a . Если а > 1, то 1/a < 1, и тогда эта прогрессия убывающая, и потому член ее при неограниченном удалении от начала ряда стремится к 0; если же а < 1, то 1/a > 1, и тогда прогрессия возрастающая и потому член ее, удаляясь от начала ряда, стремится к ∞. Таким образом, мы можем написать: а—∞ = 0 , если а >1; а—∞ = ∞, если а <1 е) Если х стремится к нулю, то степень ах стремится к 1 (и при а >1, и при а< 1). Если х стремится к 0, то ах стремится к а0. Но что представляет собой в этом случае выражение а0? До сего времени мы считали, что а0 = 1. Но считая так, мы предполагали (Отдел 2 глава 4 § 65), что выражение а0означает частное от деления одинаковых степеней буквы а. Но теперь выражение а0 мы рассматриваем иначе, а именно, как предел, к которому стремится степень ах, когда показатель х стремится к нулю. Будет ли этот предел 1, или нет, мы сейчас увидим. Возьмем какое-нибудь основание, большее 1, напр. 10, и допустим, что показатель х все уменьшается, напр, переходит через такие значения: x = 1/2 , 1/4 , 1/8 , 1/16 ... и т.д. (мы выбрали эти значения, так как при них удобно вычислять значения степени) Тогда:
(Корни эти можно найти обыкновенным извлечением, но можно их получить и из таблицы квадратных корней, приложенной в конце этой книги.) Мы видим, что степень 10х все уменьшается, приближаясь все ближе и ближе к 1 (извлечение следующего корня квадратного дало бы 1,07, дальше 1,03,.. .)• Bозьмем теперь основание, меньшее 1, напр. 1/10 и предположим, что х попрежнему уменьшается, переходя через значения 1/2 , 1/4 , 1/8 ... и т. д.
Мы видим, что степень ( 1/10 )х все увеличивается, приближаясь все ближе и ближе к 1 (дальнейшее извлечение корня дало бы 0,92, затем 0,96,...). Удовольствуемся этими двумя примерами и примем, что пред. ах = 1, если x —> 0. Изложим строгое доказательство этого предложения, т.е. докажем, что, когда x стремится к 0, абсолютная величина разности 1 — ах делается меньше любого данного положительного числа а. Предположим сначала, что а > 1 и что х, приближаясь к 0, проходит только положительные значения. Возьмем бесконечную возрастающую Г. П.: - Член такой прогрессии, при достаточном его удалении от начала ряда, может превзойти любое данное число. Значит, при некотором достаточно большом n степень (1+α)n превзойдет число а (как бы велико это число ни было). Тогда: a < (1+α)n, откуда: n√a < n√(1+α)n т. е. Когда число х, приближаясь к 0, делается меньше дроби 1/n, тогда ах делается меньше ах < 1 + α и, следовательно, ах — 1 < α. А это означает, что пред. ах = 1, если x —> . Положим теперь, что при а > 1 показатель х стремится к 0, оставаясь отрицательным (напр., х переходит через значения — 1/2 , —1/4 , —1/8 и т.д.) .Обозначив абсолютную величину отрицательного числа х буквою х', мы можем написать:
Когда х стремится к 0, тогда и х' стремится к 0, и потому степень ах', по доказанному сейчас, стремится к 1; значит, тогда дробь Допустим, наконец, что а < 1. Возьмем тогда вспомогательное число а', обратное числу а, т. е. число а' = 1/а > 1. Тогда а = 1/а' и
Так как а' > l, то, по доказанному сейчас, (а')х—> 1, когда х—>0; значит, ах—>1/1 = 1 Итак, во всех случаях ах—>1, если х —> 0. Понятие об иррациональном показателе. 263. Выражению аα, в котором α какое-нибудь иррациональное число, придают смысл только тогда, когда основание степени a есть какое-нибудь положительное число, не равное 1. При этом могут представиться следующие 3 случая: а) а > 1 и α положительное иррациональное число, напр. 10√2 Обозначим через α1 любое рациональное приближенное значение числа α, взятое с недостатком, и через α2 любое приближенное рациональное значение числа α, взятое с избытком. Тогда степень аα означает такое число, которое больше всякой степени 101,4, 101,41, 101,414, 101,4142, в котором показатели — десятичные приближенные значения √2 взятые с недостатком, но меньше каждого из чисел ряда: 101,5, 101,42, 101,415, 101,4143, в котором показатели — десятичные приближения √2 , взятые с избытком. Таким образом, если иррациональное чисто а заключено между двумя рациональными числами α1 и α2 то и степень аα заключена между степенями б) a < 1 и α попрежнему положительное иррациональное число, напр. 0,5√2. Тогда под степенью аα разумеют такое число, которое меньше всякой степени . Так, 0,5√2 есть число, меньшее каждого из чисел ряда: 0,51,4, 0,51,41, 0,51,414, 0,51,4142,. .. но больше каждого из чисел ряда: 0,51,5, 0,51,42, 0,51,415, 0,51,4143,... в) а >< 1 и α отрицательное иррациональное число; напр., 10 —√2, (1/2) —√2. Тогда выражению аα придают тот же смысл, какой имеют степени с отрицательными рациональными показателями. Так:
При подробном рассмотрении теории иррациональных показателей обнаруживается, что все свойства показателей рациональных применимы и к показателям иррациональным; так: а α • а β = а α+β ; (а α )β = а αβ Равным образом все свойства степеней с рациональными показателями, указанные нами в предыдущем параграфе, принадлежат и степеням с иррациональными показателями. Показательная функция. 264. Определение. Показательной называется функция у = ах, представляющая собою степень, у которой основание а есть постоянное положительное число, не равное 1,а показатель х - переменное число, могущее принимать всевозможные значения, положительные и отрицательные, целые и дробные, рациональные и иррациональные. При этом предполагается, что в том случае, когда х равен дроби и, следовательно, когда ах означает радикал некоторой степени, то из всех значений радикала берется только одно арифметическое, т. е. положительное. Основание а предполагается не равным 1, так как при а =1 степень ах при всяком значении х равнялась бы 1, и тогда она не зависела бы от х. Основание а предполагается еще и положительным, так как при а < 0, степень ах для многих значений х не давала бы никакого вещественного числа. Напр., при а = — 4 и при x = 1/2 степень ах обратилась бы в (— 4)½ = √— 4, что составляет мнимое выражение. Из того, что мы знаем о показателях степени, следует, что функция у = ах при всяком значении х возможна и имеет единственное значение (благодаря условию брать для радикалов только арифметическое значение). Надо обратить еще внимание на то, что если показатель х изменяется очень немного, то и степень ах изменяется тоже немного, и изменяется тем меньше, чем меньше изменение х. Напр., если х увеличим на какое-нибудь число α, то степень ах сделается ах+α, и, следовательно, она изменится на разность ах+α— ах, которую можно представить в виде произведения: ах+α— ах= ах (аα — 1) Когда α будет уменьшаться, приближаясь к нулю, тогда, как мы видели, число аα стремится к 1, и, значит, разность аα — 1 будет стремиться к нулю. Так как при этом число аx остаётся без изменения, то написакное нами произведение, в котором множимое остается без изменения, а множитель стремится к нулю, тоже стремится к нулю. Но это произведение выражает разность ах+α— ах; значит, изменение степени ах может быть, при достаточно малом α, как угодно мало; другими словами, функция ах при непрерывном изменении х изменяется тоже непрерывно. 265. График показательной функции. Построим графики следующих трех показательных функций: 1) y = 2х; 2) у = (1/2)х; 3) y = 10х. Для построения графиков первых двух функций мы дадим переменному числу х ряд целых значений: — 3,—2,—1, 0, 1, 2, 3. При х = 3 мы получим:
Подобно этому вычислим значения у и для всех остальных значений х. Добавим еще предельные значения при х = — ∞ и при х = ∞. Согласно свойствам (г) и (д), указанным в § 262, мы будем иметь: 2— ∞ = 0 ; (1/2)— ∞ = ∞; 2∞ = ∞ ; (1/2)∞ = 0; Для функции y = 10х неудобно брать указанные значения числа х, так как мы получили бы тогда для у такие большие числа, которые на чертеже не умещаются (напр., при x = 3 мы получили бы у = 103=1000). Для этой функции мы возьмем такие дробные значение (заключающиеся между —1 и + 1) x = —1 , — 3/4 , — 2/4 , — 1/4 , 0 , 3/4 , 2/4 , 1/4 , 1 Соответствующие значения у вычислим в такой последовательности:
(Эти корни можно найти и по таблице квадратных корней, приложенной в конце этой книги.) Далее, простым умножением и делением находим:
Выпишем все найденные значения в следующих трех таблицах: 1) y = 2х
2) у = (1/2)х;
3) y = 10х
(в последней таблице числа округлены). Нанеся эти значения на чертеж (кроме, конечно, предельных) и проведя через полученные точки непрерывные кривые, мы получим три графика взятых функций (всего удобнее чертеж выполнить на миллиметровой бумаге, беря за единицу длины сантиметр).
266. Свойства показательной функции. Рассматривая графики показательных функций, мы видим на них в наглядном изображении все те свойства степени а; которые были указаны ранее (§ 262). Так: 1) При всяком основании функция ах положительна (все кривые расположены выше оси х - ов). 2) При а > 1 функция ах > 1, если х > 0, и ах < 1, если х < 0; при a < 1 заключения обратны. 3) При возрастании х до + ∞ функция ах возрастает до ах , если a >1, и убывает до 0, если a < 1 (но никогда, однако, нуля, не достигает). 4) При убывании х до — ∞ функция ах убывает, стремясь к 0, если a >1, и возрастает д+ ∞, если a < 1. 5) Если х = 0, то ах = 1 при всяком а (все кривые проходят через одну и ту же точку, лежащую на оси y-ов на расстоянии от точки 0 на +1). 6) При a >1 функция при возрастании х возрастает тем быстрее, чем больше а (кривая при а = 10 поднимается вверх значительно больше, чем при а = 2).
|
означает корень, показатель которого есть знаменатель, а показатель подкоренного числа — числитель дробного показателя (т. е.n√
.
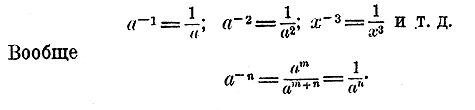
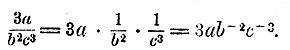
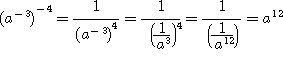
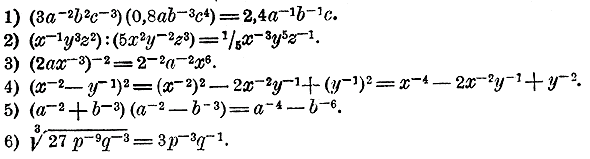
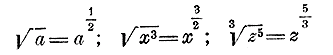
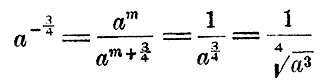
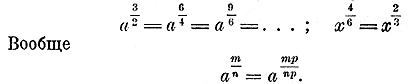
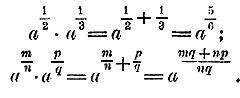
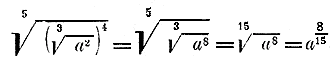
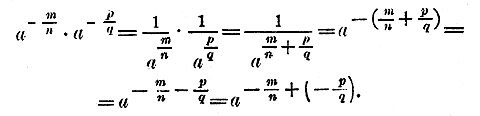
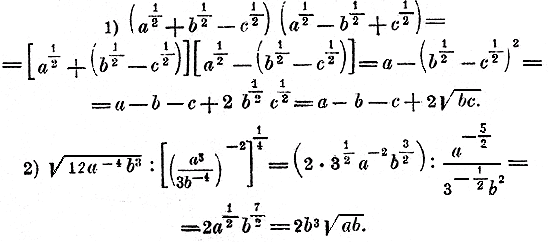
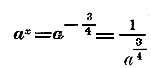
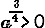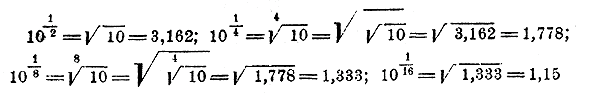
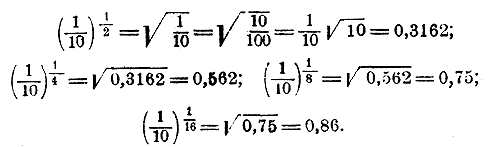Тогда:
[согласно свойству (в)]; следовательно, тогда 
стремится к 1/1, т. е. к 1. Таким образом, и в этом случае пред. ах = 1.
, но меньше всякой степени 
. Напр. 10√
