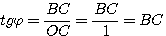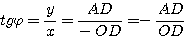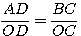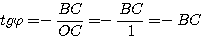ТРИГОНОМЕТРИЧЕСКИЙ КРУГ. ОСИ ТАНГЕНСОВ И КОТАНГЕНСОВ.

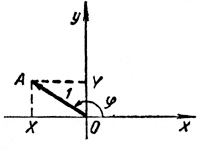
Синус и косинус угла φ мы определили отношениями:

sinφ=  ^y/_r , cosφ = ^x/_r            (1)

где х и  у — координаты  вектора,  образующего с осью абсцисс угол φ, а r — его длина. Поскольку отношения  ^y/_r и ^x/_r не зависят от длины вектора, то в качестве r можно выбрать любое положительное число. Удобнее всего положить r = 1. Тогда формулы  (1)  принимают наиболее простой вид:

sinφ = у,       cosφ = х.        (2)

Синус угла φ равен ординате, а косинус — абсциссе вектора единичной  длины, исходящего из начала координат и образующего с осью Ох угол φ.

Мы доказали, что координаты вектора не превышают по  абсолютной  величине  длины этого вектора.   Поэтому из  (2) следует, что синус и косинус любого угла не могут принимать значений, больших по абсолютной величине, чем 1.

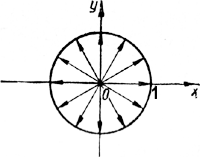
Все векторы единичной длины целиком лежат в круге радиуса 1 с центром в начале координат . Этим кругом удобно пользоваться при изучении тригонометрических функций (особенно синуса и косинуса). Поэтому он получил специальное название — тригонометрический  круг.

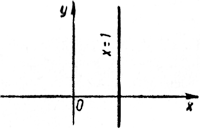
Прямая х = 1  называется осью тангенсов.

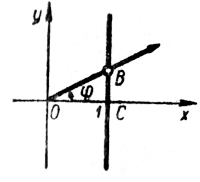
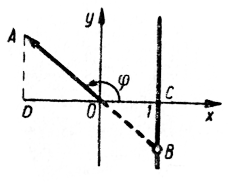
Каждому углу φ ≠  90° (2n + 1) можно поставить в соответствие точку В на оси тангенсов. Это точка пересечения конечной стороны угла φ (или ее продолжения) с осью тангенсов.

Тангенс угла φ равен ординате соответствующей точки В на оси тангенсов.

Действительно, если угол φ оканчивается в 1-й четверти , то согласно формуле (7), раздела определение тригонометрических функций

Но ВС как раз и есть ордината точки В.

Если угол φ оканчивается во 2-й четверти , то, выбирая  на его конечной   стороне    произвольную точку А и  рассматривая вектор ОА, получаем:

Из   подобия   треугольников ОАD и  ОВС следует,  что

  Поэтому

Но —ВС как раз и есть ордината  точки  В.

Аналогично можно доказать справедливость нашего утверждения и для углов φ, оканчивающихся в 3-й и 4-й четвертях.

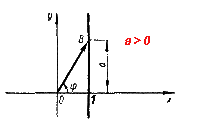
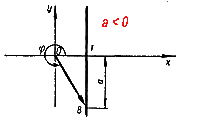
В отличие от sin φ и cos φ, принимающих только значения от —1 до 1 (включая эти два значения), tgφ может быть равен любому действительному числу. В самом деле, каким бы ни было число а, всегда, выбирая на оси тангенсов точку В с ординатой а и соединяя ее с точкой О, мы получаем вектор ОВ,образующий с осью х некоторый угол φ.

Тангенс этого угла равен а . Поэтому для любого числа а можно указать такой угол φ,  что tg φ = а.

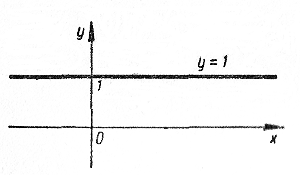
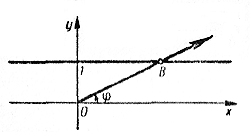
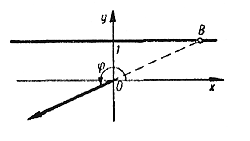
Прямая   у = 1  называется осью котангенсов.

Каждому углу φ ≠  180°n  можно поставить в соответствие точку В на оси котангенсов, являющуюся точкой пересечения конечной стороны угла φ (или ее продолжения) с осью котангенсов .

Котангенс угла φ равен абсциссе соответствующей точки В на оси котангенсов.

Это   утверждение мы предлагаем учащимся доказать самостоятельно.

Как и tgφ, котангенс угла может быть равен любому действительному числу.

Упражнения

1.  Используя тригонометрический круг, показать, что   для любого острого угла α

sin α. + cos α > 1.

2. Показать, что углам 35° и 215° соответствует одна и та же точка на оси тангенсов.
То же для углов 215° и —145°.

3. Используя  ось  тангенсов  и  ось   котангенсов,   показать, что tg 45° = tg 225° = 1.

4. Верны ли утверждения:

а)  каждому  углу φ соответствует одна вполне определенная точка оси тангенсов;

б)  каждой  точке оси   тангенсов   соответствует   один   вполне определенный  угол φ?

5. Может ли синус некоторого угла равняться ^π/₃?

6. Может ли секанс некоторого угла равняться ^π/₄?

7. Докажите геометрически, используя ось тангенсов и ось котангенсов, что для любого острого угла φ

tgφ · ctgφ = 1.