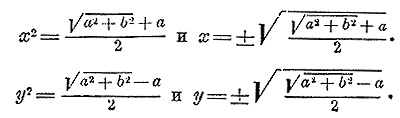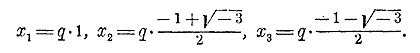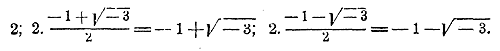| АЛГЕБРА В НАЧАЛО |
|
ОТДЕЛ ВОСЕМНАДЦАТЫЙ. ДОБАВЛЕНИЯ. Глава первая.Однозначность первых четырех алгебраических действий. Глава первая. Однозначность первых четырех алгебраических действий. 384. Предварительные разъяснения. Как мы говорили прежде (ч. I, отдел 1 глава 4 § 36), два алгебраических выражения называются тождественными, если при всяких численных значениях букв они имеют одну и ту же численную величину. Для обозначения тождественности двух выражений иногда употребляют особый знак ( = ), который ставят между тождественными выражениями Напр., пишут: (а + b) (а — b) = а2 — b2 желая этим выразить, что произведение (а + b) (а — b) равно разности а2 — b2 не при каких-либо частных значениях букв а и b, а при всевозможных. Знак этот, впрочем, большею частью заменяется обыкновенным знаком равенства (=). Все равенства, которые мы выводили в предыдущих главах для преобразования алгебраических выражений, представляют собою тождества, т.е. равенства тождественных выражений. Таковы, напр., равенства: m + (а — b + с) = m + а — b + с (ч. I, отдел2 глава2 § 48) m — (а — b + с) = m — а + b — с (ч. I, отдел2 глава2 § 50) (а + b — с) (m — n) = am — an + bm — bn — cm + cn (ч. I, отдел2 глава3§ 56). Выводя эти равенства и основанные на них правила алгебраических действий, мы однако не задавались вопросом, однозначны ли эти действия, или многозначны. Напр., мы вывели правило, что для умножения многочлена на многочлен надо умножить каждый член множимого на каждый член множителя и полученные произведения сложить. Таким образом, применив это правило к двум данным многочленам, мы должны получить такой третий многочлен, который при всевозможных численных значениях букв равен произведению данных многочленов при этих значениях букв. Но мы при этом не задавались вопросом, нельзя ли каким-нибудьь другим путем найти еще иной многочлен, который также тождественно равнялся бы произведению данных многочленов, а до тех пор, пока мы не решили этого вопроса, мы остаемся в неизвестности, однозначно ли алгебраическое умножение многочленов, или, быть-может, двузначно и даже многозначно. Такой же вопрос возникает и о других алгебраических действиях. В этой главе мы займемся разрешением указанного вопроса и прежде всего установим признак, по которому можно узнать, когда два многочлена тождественны между собою. 385. Некоторые замечания о многочленах. Во всякое алгебраическое выражение могут входить числа, выраженные цифрами, и числа, выраженные буквами. Последние могут быть двоякого рода: или это постоянные числа, предполагаемые данными, или же это переменные числа, величину которых мы можем произвольно изменять. Постоянные числа обыкновенно обозначаются первыми буквами алфавита (а, b, с, . . .), а числа переменные — последними (х, у, z, . . .)..Всякий целый многочлен, можно сказать, представляет собою алгебраическую сумму одночленов вида A xm yn z p ..., где буквы х, у, z... означают произвольные переменные,числа, а коэффициент А и показатели степени m, n, р... —какие-нибудь постоянные числа, причем показатели предполагаются числами целыми положительными (в частных случаях некоторые из них и даже все могут быть нулями). Мы будем предполагать что в многочленах, о которых нам придется говорить в этой главе, сделано приведение подобных членов. Ecли коэффициенты членов многочлена сделаются равными нулю, кроме какого-нибудь одного, то многочлен обратится в одночлен, так что можно сказать, что одночлен есть частный случай многочлена. Сумма всех показателей при переменных числах в одночлене называется степенью его, или измерением. Тот член многочлена, которого степень наибольшая, называется высшим членом его, а тот, которого степень наименьшая, называется низшим членом. Степенью самого многочлена называется степень его высшего члена. Если все члены одного измерения, то многочлен называется однородным. Тот член многочлена, который совсем не содержит переменных (иначе сказать, член нулевой степени), называется свободным членом. Приведем некоторые примеры многочленов: 1) 2х— 5 двучлен 1-й степени; 2) х2 — 3х + 6 трехчлен 2-й степени; 3) 3х4 + 1/2 х2 — х + 10 неполный многочлен 4-й степени (не содержит члена с х3), 4) Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L общий вид многочлена m-й степени, содержащего одно переменное и расположенного по убывающим степеням этого переменного; 5) х2— 3ху + y2 однородный трехчлен 2-й степени с двумя переменными; 6) 4хy2z + х3 — х2у— 2xyz + 5x многочлен 4-й степени с 3 переменными (не содержит свободного члена). 386. Лемма. Если целый многочлен с одним переменным х (обозначим его для краткости одной буквою М): М= Ахm + Bхm - 1 + Cхm - 2 + ... + Kх не содержит свободною члена, то всегда можно найти такое значение х не равное нулю, при котором абсолютная величина этого многочлена будет как угодно мала, т.е. она будет меньше любого положительного числа а, как бы мало последнее ни было. Доказательство. Очевидно, что абсолютная величина многочлена меньше суммы абсолютной величины всех его членов (или в крайнем случае равна ей). С другой стороны, если для х будем брать положительные числа, меньшие 1, то х2 < х, х3 < х, х4 < х; и т. д. Поэтому, обозначив абсолютные величины чисел M, А, В, С...и х буквами: M', А', В', С'...и х', мы можем написать: M' < А'х' + В'х' + Cх' +...+ K'х' , т. е. M' < (A' + B' + C'+.. .+ K') х' (при х' < 1). Из этого неравенства видно, что если для х' возьмем какое- нибудь положительное число, которое, будучи меньше 1, в то же время и меньше частного а : (A' + B' + C'+.. .+ K') , то тогда M' сделается меньше а, что и требовалось доказать. Напр., многочлен х4 — 3х3 + х2 — 2х сделается по абсолютной величине меньше 0,000001, если для х возьмем какое-нибудь положительное число, меньшее частного 0,000001: (1 + 3 +1 + 2), т. е. меньше 1/7 миллионной. 387. Теорема. Для того чтобы целый многочлен тождественно равнялся нулю (т. е. равнялся нулю при всяких численных значениях переменных), необходимо и достаточно, чтобы коэффициенты всех его членов были нули. Доказательство. Сначала докажем эту теорему для многочлена М с одним переменным: M = Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L. 1) Необходимость признака. Предположим, что М=0 при всяких значениях х; покажем, что тогда коэффиценты всех его членов (и свободный член L) должны быть нули. Если М=0 при всяких значениях х, то М =0 и при х = 0. Но при этом значении х многочлен М обращается в L; значит, тогда L = 0. Теперь данный многочлен можно представить так: М = х(Ахm + Bхm - 1 + Cхm - 2 + ... + Iх+ K) или М = х( N + K ) если положим: N= Ахm + Bхm - 1 + Cхm - 2 + ... + Iх Так как M = 0 при всяких значениях х, то M = 0 и при всех значениях х, отличных от нуля. Но при таких значениях произведение х( N + K ) может равняться нулю только тогда, когда N + K = 0. Это возможно только тогда, когда K = 0. В самом деле, допустим временно, что K =/= 0. Тогда, согласно доказанной выше лемме, можно для х найти такое значение (отличное от нуля), при котором абсолютная величина многочлена N, не содержащего свободного члена сделается меньше абсолютной величины K; при таком значении х алгебраическая сумма N + K, очевидно, не может равняться нулю. Значит, необходимо, чтобы K=0. Представив теперь данный многочлен так: М = х2 (Ахm - 2 + Bхm - 3 + ... + I) мы таким же путем докажем, что I=0 и т. д., т. е. окажется, что все коэффициенты должны быть нули. 2) Достаточность признака. Пусть все коэффициенты будут нули; тогда при всяком значении х каждый член многочлена равен нулю, и поэтому M = 0. Докажем теперь теорему для многочлена с 2 переменными x и у. Расположим его члены по убывающим степеням одного какого-нибудь переменного, напр., х; тогда многочлен будет иметь вид: Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L (1) где буквы А, В, С... L означают некоторые многочлены (или одночлены), содержащие переменное у, причем коэффициенты этих многочленов принадлежат к коэффициентам данного многочлена1). Дадим теперь переменному у какое-нибудь частное значение, у0. Тогда коэффициенты А, В C,... получат некоторые частные значения, которые мы обозначим А0 , В0, C0...L0, и многочлен будет: А0хm + B0хm - 1 + C0хm - 2 + ... + L0 (2) : Допустим, что многочлен (1) обращается в нуль при всевозможных значениях х и у; но тогда он обращается в нуль при у = у0 и любом значении х. Значит, многочлен (2) обращается в 0 при всяком значении х. Поэтому, по доказанному выше, А0 = 0, В0 = 0, ... L0 = 0. Но так как у0 мы взяли произвольно, то многочлены А, В, С... L (с одним переменным у) должны быть равны 0 при всяком значении у, а для этого нужно, чтобы все ; коэффициенты этих многочленов были нули. Но коэффициенты эти служат также и коэффициентами данного многочлена; значит, последние должны быть нули. Достаточность признака очевидна сама собою. После этого тем же приемом докажем теорему и для 3 переменных, потом для 4 и т. д, Теперь мы можем легко установить следующий закон тождества многочленов. 388. Теорема. Для того, чтобы два целых многочлена были тождественны, необходимо и достаточно, чтобы они ничем не различались друг от друга, кроме порядка их членов. Доказательство. Сначала докажем теорему для многочленов с одним переменным. Пусть нам дано тождество: Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L = Pхn + Qхn - 1 + ... + Rх + S Предположим, что m не равно n; допустим, напр., что m = n + 2. Тогда можно написать: Ахn + 2 + Bхn + 1 + Cхn + ... + Kх + L = Pхn + Qхn - 1 + ... + Rх + S Если эти два многочлена равны друг другу при всяком значении х, то их разность тождественно равна, нулю; значит; Ахn + 2 + Bхn + 1 + (C — Р)хn + (D — Q)хn - 1+ ... + (L — S) = 0. Для этого, согласно предыдущей теореме, необходимо и достаточно, чтобы A = 0, В = 0, C = P, D = Q,... L = S. Но тогда эти многочлены ничем не различаются (кроме, быть может, порядка их членов). Таким же путем можно доказать теорему и для нескольких переменных. 389. Однозначность алгебраического сложения, вычитания и умножения многочленов. Докажем однозначность для какого-нибудь одного из этих трех действий, напр., для умножения; для других действий можно повторить то же самое. Положим, что умножая многочлены М и N по известному правилу умножения многочленов, мы получили некоторый многочлен Р. Допустим теперь, что каким-нибудь другим путем можно получить еще иной многочлен P', также тождественно равный произведению MN. Так как оба многочлена Р и Р' тождественны одному и тому же произведению MN, то, очевидно, они должны быть тождественны и между собою, а для этого, согласно закону тождества, необходимо и достаточно, чтобы Р и Р' ничем друг от друга не различались (кроме порядка их членов), т. е чтобы эти многочлены представляли собою в сущности один и тот же многочлен. Значит, алгебраическое умножение есть дейотвие однозначное. То же рассуждение можно применить к сложению и вычитанию. Докажем теперь и однозначность деления многочленов. 390. Однозначность алгебраического деления многочленов. Под делением многочлена M на другой многочлен N в общем случае разумеют нахождение таких двух многочленов Q (частное) и R (остаток), которые удовлетворяли бы тождеству: M= NQ + R, причем степень остатка R была бы ниже степени делителя N Если степень делителя N не выше степени делимого М, то такое деление возможно, как это видно из способа деления многочленов, указанного в отдел2 глава 4§ 70 (часть I). Если окажется, что R есть нуль, то это будет деление без остатка; и тогда деление есть действие (обратное умножению), посредством которого по данному произведению (делимому) и одному из сомножителей (делителю) отыскивается другой сомножитель (частное). Если же R =/= 0, то это будет деление с остатком (аналогичное делению с остатком одного целого числа на другое). Покажем теперь, что деление с остатком и деление без остатка суть действия однозначные. Предположим, что помимо многочленов Q и R (найденных так, как это описано в отдел2 глава 4§ 70, ч. I) существуют еще многочлены Q' и R' также удовлетворяющие тождеству: M= NQ' + R' Тогда мы будем иметь тождество: NQ + R = NQ' + R' откуда: NQ—NQ'=R' — R т.е. N(Q — Q') = R'—R. Последнее тождество возможно только тогда, когда многочлены Q' и R' не отличаются соответственно от многочленов Q и R. В самом деле, если бы многочлен Q' разнился от многочлена Q, то тогда левая часть последнего тождества, по раскрытии скобок, представляла бы собою некоторый многочлен степени не ниже степени N, тогда как правая часть этого тождества была бы многочленом степени, ниже степени N (так как, пo определению делениz, cтепень R и сnепень R' ниже степени N); а два многочлена разных степеней не могут быть тождественными, как это следует из закона тождества. Итак многочлены Q и Q' не могут быть различными; но тогда левая часть тождества равна нулю; потому и правая часть его равна нулю, следовательно и R не может разниться от R'. Таким образом, частное может быть только одно, и остаток может быть только один, т. е. деление есть тоже действие однозначное. Заметим, что когда деление М на N совершается без остатка (R =0), то говорят просто, что M делится на N Делимость многочлена, целого относительно х на разность х — а. 391. Теорема. Многочлен, целый относительно х (и расположенный по убывающим степеням этой буквы) M = Ахm + Bхm - 1 + Cхm - 2 + ... + K. при делении на разность х — а (где а есть произвольное число, положительное или отрицательное) дает остаток R = Аam + Bam - 1 + Cam - 2 + ... + K равный тому значению делимого, которое оно получает при х = а. Доказательство. Пусть от деления М на х — а получается некоторое частное Q и некоторый остаток R. Так как, по определению деления, степень остатка R должна быть ниже степени делителя х — а, а этот делитель 1-й степени, то степень R должна равняться нулю, т. е. R не содержит в себе х. Заметив это, возьмем тождество: М = (х — a)Q + R, которому, согласно определению деления, должны удовлетворять Q и R. Если это равенство есть тождество, то это значит, что оно верно при всевозможных значениях х, а потому оно должно быть верно и при х = а. Но при х = а оно дает: М' = (a — a)Q' + R, если буквами М' и Q' обозначим те значения М и Q, которые эти многочлены принимают при х — а (остаток R, как не содержащий вовсе х, не изменится от подстановки а на место х). Так как при х = а произведение (х — a)Q обращается в 0 • Q, что равно 0, то последнее равенство дает: М' = R, т. е. R = Аam + Bam - 1 + Cam - 2 + ... + K, что и требовалось доказать. Следствие. Так как х + а = х — (— а), то, применяя доказанную теорему к сумме х + а, найдем: многочлен Аxm + Bxm - 1 + Cxm - 2 + ... + K при делении на сумму х + а дает в остатке число, равное А(—a)m + B(—a)m - 1 + ... + K, т. е. число, равное тому значению делимого, которое оно получает при х = — а Примеры. 1) Многочлен х5 — 3х2 + 5х — 1 при делении на х — 2 дает остаток, равный 25 — 3•22 + 5•2 — 1= 29. 2) Многочлен х5 — 3х2 + 5х — 1 при делении на х + 2 дает остаток: 392. Теорема. Для того, чтобы многочлен Аxm + Bxm - 1 + Cxm - 2 + ... + K делился на разность х — а, необходимо и достаточно, чтобы при х — а он обращался в нуль. Доказательство. Это необходимо, так как если указанный многочлен делится на х — а, то остаток от деления должен быть 0 , а этот остаток по доказанному выше, есть то значение делимого, которое оно принимает при х = а. Это достаточно, так как если многочлен обращается в 0 при х = а, то это значит, что остаток от деления этого многочлена на х — а равен 0. Следствие. Для того, чтобы многочлен Аxm + Bxm - 1 + ... + K делился на сумму х + а, необходимо и достаточно, чтобы при х = — а он обращался в 0, так как сумма х + а есть разность х — (— а). Примеры. 1) Многочлен х3 — 4х2 + 9 делится на x — 3, потому что 33 — 4•32 + 9=0 2) Многочлен 2х2 + х — 45 делится на х + 5, так как 2•(— 5)2 + (— 5) — 45= 0. 393. Теорема. Зная один корень алгебраического уравнения: Аxm + Bxm - 1 + Cxm - 2 + ... + K= 0, мы можем понизить степень этого уравнения на 1. Действительно допустим, что каким-нибудь путем (напр., просто догадкой) мы нашли один корень х = а. Это значит, что многочлен, стоящий в левой части уравнения, обращается в 0 при х = а. Но тогда этот многочлен делится на х — а. Сделав это деление, мы получим в частном некоторый многочлен Q степени m — 1. Теперь данное, уравнение можно представить так: Q(x — a) = 0. Это уравнение удовлетворяется только теми значениями х, при которых либо х — а равно 0, либо Q равно 0. Приняв, что х—а = 0, мы получим ранее найденный корень, если же допустим, что Q=0, то будем иметь уравнение, степень которого на 1 ниже степени данного уравнения. 394. Некоторые особые случаи деления двучленов. 1) Разность одинаковых степеней двух чисел делится на разность тех же чисел, так как xm — am при делении на х — а дает остаток am — am, т. е. 0. 2) Сумма одинаковых степеней двух чисел не делится на разность этих чисел, так как xm + am при делении на х — а дает остаток am + am = 2am, а не 0. 3) Разность одинаковых четных степеней двух чисел делится, а нечетных не делится на сумму этих чисел, так как при делении разности xm — am на х + а остаток равен (— am )— am , чтo при m четном равно нулю, а при m нечетном составляет —2am. 4) Сумма одинаковых нечетных степеней двух чисел делится, а четных не делится на сумму этих чисел, так как при делении суммы xm + am на х + а остаток равен (— am )+ am, что при m нечетном равно 0, а при m четном составляет 2am. Примеры. 1) x1 + a1 делится на х + а, но не делится на х — а; 2) x2 — a2 делится и на х — а, и на х + а; 3) x2 + a2 не делится ни на х — а, ни на х + а 4) x3 — a3 делится на х — а, но не делится на х + а 5) x3 + a3 делится на х + а, но не делится на х — а;. Замечание. Разность xm — am при m четном делится и на х — а, и на х + а; в таком случае эта разность должна делиться на произведение (х — а) (х + а), т. е. на x2 — a2. И действительно, представив разность x2n — a2n в таком виде: (x2)n — (a2)n, мы замечаем, что это есть разность одинаковых степеней чисел x2 и a2; следовательно, она должна делиться на разнисть этих чисел, т. е. на x2 — a2. Так, x4 — a4 = (x2 — a2) (x2 + a2), x6 — a6 = (x2 — a2) (x4 + a2x2 + a4 ) и т. п. 395. Частные, получаемые при делении xm ± am нa х ± а. Из рассмотрения процесса деления:
замечаем, что многочлен, получившийся в частном, содержит m членов; сумма показателей в каждом члене при а и х одна и та же, именно m — 1; показатели х идут, уменьшаясь на 1, от m — 1 до 0, показатели же а идут, увеличиваясь на 1, от 0 до m — 1; коэффициенты у всех членов равны 1; знаки все +; число членов в частном m. Заметив это, можем прямо пиоать: x3 — a3 = (x — a) (x2 + ax + a2 ) ; и т. п. Чтoбы полyчить частное от деления xm — am нa х + а при m четном или при делении xm + am нa х + а при m нечетном, достаточно в полученном выше частном заменить а на — а. Таким образом: x3 + a3 = (x + a) (x2 — ax + a2 ) ; и т. п. Общие формулы решения системы двух уравнений первой степени с двумя неизвестными. 396. Общие формулы. Сиcтему 2 уравнений 1 степени с 2 неизвестными мы можем в общем виде изобразить так (ч. 1, отдел 5 глава 1 § 138): ах + bу = с Решим эту систему, предполагая, что ни один из 4 коэффициентов а, b, a', b' не равен нулю. Применим, например, cпособ сложения или вычитания. Умножив члены первого уравнения на b', а члены второго на b, вычтем второе уравнение из первого:
Умножив члены первого уравнения на а' , а второго на а вычтем уравнения почленно:
Знаменателей обеих формул можно сделать одинаковыми, если оба члена дроби, полученной для у, умножим на —1; тогда получим следующие общие формулы:
Полезно запомнить, как можно составить формулы для неизвестных, не прибегая каждый раз к их выводу. Знаменатель аb' — а'b, одинаковый для обеих формул, составлен из коэффициентов:
перемножением их крест-накрест, причем одно произведение взято с + , другое с —. Числители формул получаютоя из знаменателя заменою в нем коэффициентов определяемого неизвестного соответственно свободными членами с и с'. Чтобы получить, например, числителя формулы х, надо в знаменателе аb' — а'b заменить иксовы коэффициенты а и а' соответственно на с и с'; от этого получим: cb' — c'b. 397. Исследование общих формул. Рассмотрим особо следующие 2 случая: I. Обший знаменатель аb' — а'b не равен нулю. В этом случае для каждого неизвестного получается единственное решение, которое может быть положительным, отрицательным и равным нулю. О значении этих решений здесь может быть сказано то же самое, что говорилось при исследовании одного уравнения с одним неизвестным (ч. I, отдел 4 глава 2 §§ 126, 127 и 128). II. Обший знаменатель аb' — а'b равен нулю. Докажем, что тогда; а) Если одно неизвестное представляется под видом 0/0, то и другое неизвестное представляется под тем же видом. Пусть, например, x = 0/0. Для этого нужно, чтобы cb' = c'b Перемножив эти два равенства крест-накрест, найдем: cb' a'b = c'bab' ; откуда: cb' a'b — c'bab' = 0, или bb'(а'с — ас') = 0. Так как числа b и b', по предположению, не равны нулю, то последнее равенство возможно только тогда, когда а'с — ac' = 0; но тогда и у = 0/0. Также, если допустим, что у = 0/0 , т. е. ас' = а'с и аb' — а'b, то, перемножив эти равенства крест-накрест найдем: ac'a'b=a'cab', откуда аа' (с'b — cb') = 0. Так как числа а и а' мы предположили не равными 0, то последнее равенство дает: с'b — cb' = 0, а тогда и х = 0/0. б) Если одно неизвестное представляется под видом m/0, где m =/= 0, то и другое неизвестное представляется под видом n/0, где n =/= 0. Действительно, если бы оно приняло вид 0/0, то и первое неизвестное, по доказанному, имело бы тот же вид, а мы предположили, что этoго нет. Решения: х = 0/0 и у = 0/0 означают неопределенность задачи. Действительно, умножив все члены первого уравнения на b' а члены второго на b (что можно сделать, так как числа b и b' по предположению, не равны 0), получим: аb'х + bb'у = сb' Если х = 0/0 и у = 0/0, то ab' = a'b, сb' = c'b; тогда эти два уравнения представляют собою одно уравнение с 2 неизвестными; а в этом случае неизвестные могут иметь бесчисленное множество значений. Решения: х = m/0 и у = n/0 означают несовместность уравнений. В самом деле, если ab' = a'b, a сb' =/= c'b то левые части последних уравнений имеют одинаковые чиcленные величины, а правые — разные; значит, эти уравнения несовместны, и задача невозможна. Из сказанного заключаем: система двух уравнений первой степени с 2 неизвестными допускает или одно определенное решение, или бесчисленное множество решений, или же ни одного решения. 398. Случай, когда некоторые из коэффициентов равны нулю. В этом случае не следует полагаться на общие формулы (выведенные в предположении, что ни один из коэффициентов а, b, а' и b' не равен нулю), а должно подвергать каждый случай особому исследованию. Положим, например, что оба коэффициента при одном и том же неизвестном равны нулю. Пусть b = b' = 0; тогда ab' — a'b = 0 и сb' — c'b = 0, и общие формулы дают х = 0/0, y = m/0 или 0/0, смотря по тому, будет ли ас' не равно или равно а'с. Уравнения же в этом случае дают:
Если ас' не равно а'с, то c/a не равно c'/a' , и уравнения невозможны, потому что для х получаются два различные значения; между тем в этом случае формулы для неизвестных дают х = 0/0, y = m/0 . Если же ас' = а'с, то c/a = c'/a' тогда для х получается определенное решение, а у может иметь всевозможные значения, хотя общие формулы в этом случае дают х = 0/0, y = 0/0. Извлечение квадратного корня из многочлена. 399. Объяснение. В некоторых случаях квадратный корень из многочлена может быть выражен в виде многочлена (в виде одночлена он не может быть выражен, так как одночлен в квадрате дает одночлен, а не многочлен). Покажем это на следующем примере:
Мы расположили данный многочлен по убывающем степейям буквы а, так что высший член в нем есть первый, а низший — последний. Предположим, что существует многочлен, квадрат которого равен данному многочлену. Пусть этот многочлен тоже расположен по убывающим степеням буквы а, так что высший член в нем первый. Мы в вдели (ч. I, отдел 6 глава 2 § 155), что квадрат многочлена = квадрату 1 -го члена +удвоенное произведение 1-го члена на 2-й + квадрат 2-го члена + удвоенное произведение суммы первых двух членов на 3-й + квадрат 3-го члена, и т. д. Если возвышаемый многочлен расположен по убывающим степеням главной буквы, то очевидно, что высший член в квадрате этого многочлена есть квадрат первого его члена. В подкоренном многочлене высший член есть 16а4b2; значит, это и есть квадрат 1-го члена искомого многочлена; поэтому 1-й член корня = √16а4b2 = ± 4а2b. Таким образом: чтобы найти первый член корня, достаточно извлечь квадратный корень из первого члена подкоренного многочлена (предварительно расположенного.). Из найденных двух значений первого члена возьмем пока одно: + 4а2b, а впоследствии примем во внимание и другое.
Найдя первый член корня (4а2b) , возвысим его в квадрат и вычтем из подкоренного многочлена. В остатке (первом) должны получиться все члены многочлена, кроме первого. Мы написали только 2 члена остатка, потому что остальные пока не нужны. В этом первом остатке должны содержаться: удвоенное произведение 1-го члена на 2-й + квадрат второго члена + удвоенное произведение суммы первых двух членов на 3-й + квадрат 3-го, и т. д. Из всех этих членов высшим будет удвоенное произведение 1-го члeна на 2-ой, а в остатке высший член есть—24а3b3; следовательно—24а3b3 и есть удвоенное произведение 1 -го члена на 2-й. А потому: чтобы найти 2-й член корня, достаточно разделить первый член первого остатка на удвоенный первый член корня. Для этого налево от остатка (или направо от него) проводим вертикальную черту, за нею пишем удвоенный первый член корня (8а2b). Разделив—24а3b3 на 8а2b, получаем одночлен — 3аb2, который и записываем в корне на месте второго члена, и вместе с тем приписываем его за вертикальной чертой к удвоенному первому члену (получаем за чертой 8а2b — 3аb2). Это делается для того, чтобы, умножив 8а2b — 3аb2 на — 3аb2, зараз получить: удвоенное произведение 1-го члена на 2-й и квадрат 2-го члена. Умножив на самом деле 8а2b — 3аb2 на — 3аb2, пишем произведение под остатком и из него вычитаем (для чего переменяем знаки у вычитаемого многочлена на противоположные); получаем второй остаток + 4а2b4 — 3аb5+ 1/4 b6 Во втором остатке должны содержаться: удвоенное произведение cуммы первых двух членов корня на 3-й член + квадрат 3-го члена, и т. д.; другими словами: удвоенное произведение 1-го члена на 3-й + удвоенное произведение 2-го члена на 3-й + квадрат 3-го члена, и т. д. Изо всех этих членов высший есть удвоенное произведение 1-го члена на 3-й; а в остатке высший член есть + 4а2b4. Значит, + 4а2b4 и есть удвоенное произведение 1-го члена корня на 3-й его член. Поэтому: чтобы найти 3-й член корня, достаточно разделить первый член второго остатка на удвоенный 1-й член корня. Пишем 8а2b за вертикальною чертою и делим на это выражение 4а2b4; В нашем примере 3-й остаток оказался 0; если бы получился остаток, не равный 0, то мы продолжали бы действие далее, рассуждая так, как и раньше. Для первого члена искомого корня мы взяли, лишь одно значение √16а4b2 , именно +4а2b ; но мы могли бы также взять и: — 4а2b; в этом случае остальные члены корня тоже переменили бы знаки на противоположные, потому что для получения их пришлось бы делить первые члены остатков не на 8а2b, а на —8а2b. Значит, квадратный корень из многочлена имеет два значения; в нашем примере одно = 4а2b — 3аb2 +1/2 b3, другое — 4а2b + 3аb2 —1/2 b3 оба эти значения можно выразить так: ±(4а2b — 3аb2 +1/2 b3) Мы могли бы подкоренной многочлен расположить по возрастающим степеням главной буквы; члены корня нашлись бы тогда совершенно так же, как сейчас было объяснено; только в объяснений слово „высший" должно заменить словом „низший". 400. Правило. Чтобы извлечь квадратный корень из многочлена, предварительно располагают его по убывающим или по возрастающим степеням одной и той же буквы. Извлекают квадратный корень из 1-го члена многочлена; полученный результат берут за 1-й член корня. Возвысив этот член в квадрат, вычитают его из данного многочлена. Делят 1-й член первого остатка на удвоенный первый член корня; полученное частное берут за 2-й член корня. Приписав этот член к удвоенному 1-му члену корня, умножают полученный двучлен на 2-й член корня и произведение вычитают из остатка. Делят 1-й член 2-го остатка на удвоенный 1-й член корня; полученное частное принимают за 3-й член корня. Приписав этот член к сумме удвоенного 1-го члена и удвоенного 2-го члена, умножают полученный трехчлен на 3-й член корня и произведение вычитают из 2-го остатка. Продолжают действие так же и далее. 401. Признаки невозможности извлечения. 1) Если, данный многочлен есть двучлен, то корень квадратный из него не может быть выражен многочленом, так как всякий многочлен в квадрате дает по меньшей мере 3 члена, а не 2. 2) Если высший или низший члены многочлена не представляют собою точных квадратов, то корень квадратный из многочлена не может быть выражен многочленом. Это прямо следует из правила нахождения высшего и низшего членов корня. 3) Если высший и низший члены многочлена — точные квадраты, то возможность или невозможность извлечения корня обнаружится посредством самого действия; при этом если многочлен расположен по убывающим степеням главной буквы, то продолжают действие до тех пор, пока в остатке не получится 0, или пока не получится остаток, у которого первый член не делится на удвоенный первый член корня; в последнем случае извлечение невозможно. Если же многочлен расположен по возрастающим степеням главной буквы, то, вычислив предварительно последний член корня (который равен корню квадратному из последнего члена многочлена), продолжают действие до тех пор, пока в корне не получится член, у которого показатель главной буквы равен показателю этой буквы в вычисленном последнем члене корня, или более его; если при этом есть остаток, то извлечение невозможно. 402. Замечание. Когда из данного многочлена нельзя извлечь точного квадратного корня, все-таки иногда бывает полезно начать извлечение с тем, чтобы, прекратив его на каком-нибудь члене корня, представить данный многочлен в виде суммы квадрата с остатком от извлечения. Например:
Положим, что мы прекратили извлечение на втором члене корня. Получившийся при этом остаток произошел от вычитания из подкоренного многочлена всех членов, которые получаются от возвышения в квадрат найденного двухчлена х2 — 2х ; значит: (х4 — 4х3 + 3) — (х2 — 2х)2 = — 4х2 + 3; следовательно, х4 — 4х3 + 3 = (х2 — 2х)2 + (— 4х2 + 3) = (х2 — 2х)2 — 4х2 + 3. Преобразование сложного радикала. 403. Корни биквадратного уравнения, как мы видели (ч. I, отдел 9 глава 3 § 229), выражаются под видом сложных радикалов Пусть в сложном радикале
в котором числа х и у положительные рациональные. Возвысив обе части этого равенства в квадрат, получим: А + √B = х + у + 2√xy = х + у + √4xy. Откуда: √4xy = (А — х — у) + √B и следовательно, 4xy = (А — х — у) 2 + B + 2(А — х — у)√B Левая часть этого уравнения есть число рациональное; значит, и правая часть должна быть числом рациональным. Но это возможно только тогда, когда коэффициент при √B будет равен нулю. Положив А— х — у = 0, находим: х + у = А; тогда 4xy = В, или: х + у = А, xy = B/4 Из этих равенств видно, что х и у можно рассматривать, как корни такого квадратного уравнения, у которого коэффициент при неизвестном во 2-й степени есть 1, коэффициент при неизвеcтном в 1-й степени есть — А, а свободный член равен B/4 (ч. I, отдел 9 глава 1 § 219). Значит, решив уравнение: z2 — Аz + B/4 = 0 найдем х и у:
Следовательно,
Отсюда видно, что радикал Подобным же образом выведем, что при тех же условиях и при A>√B :
Примеры.
(Известная геометрическая формула удвоения числа сторон правильного вписанного многоугольника). Здесь: A = 2r 2; B = 2r 2 —an2r 2; √A2—B = anr поэтому:
Дополнительные сведения о неравенствах. 404. Два рода вопросов относительно неравенств. Относительно неравенств (как и равенств), содержащих буквы, могут быть предлагаемы вопросы двоякого рода: 1) решить неравенство, содержащее неизвестные, т. е. определить, между какими пределами должны заключаться численные значения неизвестных, чтобы оно было верно, т. е. больше чего или меньше чего должны быть эти значения неизвестных; 2) доказать тождественное неравенство, т. е. обнаружить верность его при всевозможных значениях букв, или, по крайней мере, при значениях, ограниченных заданными наперед условиями. Решение обоих вопросов основывается на некоторых свойствах неравенств, подобных тем, которые служат основанием для решения уравнений. 405. Равносильные неравенства. Неравенства, содержащие одни и те же неизвестные, называются равносильными, если они удовлетворяются одними и теми же значениями этих неизвестных; так, 2 неравенства 3х + 2< х +10 и 3х < х + 8 равносильны, так как оба они удовлетворяются значениями х, меньшими 4, и только этими значениями. Относительно равносильности неравенств докажем теоремы, весьма сходные с подобными же теоремами относительно равносильности уравнений. 406. Теорема 1. Если к обеим частям неравенства (содержащего неизвестные) прибавим (или отнимем) одно и то же число, то получим новое неравенство, равносильное первому. Обозначим левую часть неравенства, содержащего неизвестные, одною буквою А и правую часть — другою буквою В, и пусть m есть какое угодно число; докажем, что два неравенства: A > В (1) А+ m > В + m (2) равносильны. Положим, что первое неравенство удовлетворяется при некоторых значениях букв. Это значит, что при этих значениях численная величина А делается больше численной величины В, но тогда при тех же значениях букв и численная величина суммы А+ m сделается больше численной величины суммы В + m , так как если к обеим частям неравенства придадим поровну, то знак неравенства не изменится. Значит, всякое решение неравенства (1) принадлежит и неравенству (2). Обратно, если при некоторых значениях букв численная величина суммы А+ m делается больше численной величины суммы В + m, то для тех же значений букв и численная величина А сделается больше численной величины В (если от обеих частей неравенства отнимем поровну, то...); следовательно, все решения неравенства (2) удовлетворяют и неравенству (1); значит, эти неравенства равносильны. Переходя от неравенства (2) к неравенству (1), мы замечаем, что от обеих частей неравенства можно отнять одно и то же число. Замечание. Число, прибавляемое к обеим частям неравенства или отнимаемое от них, можег быть дано в виде какого-нибудь буквенного выражения, причем выражение это может содержать в себе и неизвестные, входящие в неравенство; нужно только, чтобы прибавляемое выражение при всех значениях неизвестных, удовлетворяющих данному неравенству, представляла собою определенное число (а не принимало бы, например, вида 0/0 , или ∞). Следствие. Любой член неравенства можно перенести из одной части в другую с противоположным знаком. Если, например, имеем неравенство: A > В + С, то, отняв от обеих частей по С, получим: А —С > В. 407. Теорема 2. Если обе части неравенства (содержащею неизвестные) умножим (или разделим) на одно и то же положительное число, то получим новое неравенство, равносильное первому. Докажем, что два неравенства: A > В (1) Аm > Вm (2)
равносильны, если только m положительное число. Пусть при некоторых значениях неизвестных численная величина А делается больше численной величины В; тогда при тех же значениях неизвестных и численная величина произведения Аm сделается больше численной величины произведения Вm, так как от умножения обеих частей неравенства на положительное число, как мы знаем, знак неравенства не изменяется. Значит, все решения неравенства (1) удовлетворяют и неравенству (2). Обратно, если при некоторых значениях букв численная величина Аm делается больше численной величины Вm, то при тех же значениях букв и численная величина А сделается больше численной величины В, так как от деления обеих частей неравенства на положительное число знак неравенства не изменяется. Замечание. Положительное число, на которое, по доказанному, мы имеем право умножить или разделить обе части неравенства (не изменяя его знака), может быть дано в виде буквенного выражения, причем это выражение может содержать в себе и неизвестные, входящие в неравенство. Но при этом надо особо рассмотреть, при всех ли значениях букв, входящих в выражение, на которое мы умножаем или делим обе части неравенства, это выражение остается положительным числом. Например, умножим обе части неравенства A > B на выражение (x — 5)2; A > B (1) A(x — 5)2 > B(x — 5)2 (2) Множитель (x — 5)2 остается положительным числом при всех значениях х, кроме одного: х = 5. Значит, неравенства (1) и (2) равносильны в том случае, если первое из них не удовлетворяется значением х = 5; в противном же случае неравенство (1), удовлетворяясь всеми решениями неравенства (2), имеет еще свое особое решение: х = 5 (это решение, конечно, неравенству (2) не удовлетворяет). Следствие. Если обе части неравенства содержат положительный общий множитель, то на него можно сократить неравенство. Например, в обеих частях неравенства: (x — 5)2(x— 1) > (x — 5)2(3—x) есть общий множитель (x — 5)2. Этот множитель при x — 5 обращается в 0, а при всех остальных значениях х он есть число положительное. Решение х =5 не удовлетворяет данному неравенству. Желая решить, удовлетворяется ли оно при других значениях х, мы можем сократить обе части неравенства на (x — 5)2 как на число положительное; после сокращения получим: х —1 > 3 —х. Все значения х, удовлетворяющие этому неравенству, за исключением х = 5, удовлетворяют и данному неравенству. 408. Теорема 3. Если обе части неравенства (содержащего неизвестные) умножим (или разделим) на одно и то же отрицательное число и при этом переменим знак неравенства на противоположный, то получим новое неравенство равносильное первому. Эта теорема доказывается совершенно так же, как и теорема 2-я; надо только принять во внимание, что от умножения или деления обеих частей неравенства на отрицательное число знак неравенства изменяется на противоположный. По поводу этой теоремы можно высказать такое же замечание, какое было сделано по отношению к теореме 2-й. Следствия, а) Переменив у всех членов неравенства знаки на противоположные (т. е. умножив обе его части на — 1), мы должны изменить знак неравенства на противоположный. б) Нельзя умножить обе части неравенства на буквенного множителя, знак которого неизвестен. в) Неравенство с дробными членами можно привести к целому виду. Возьмем, например, такое неравенство:
Перенесем все члены в левую часть и приведем их к общему знаменателю:
Если ВD положительное число, то мы можем его отбросить, не изменяя знака неравенства, потому что отбросить ВD все равно, что умножить на это число обе части неравенства. Отбросив ВD, получим неравенство, не содержащее дробей: AB — BC > 0. Если ВD отрицательное число, то мы можем его отбросить, переменив при этом знак неравенства на противоположный; тогда снова будем иметь неравенство с целыми членами: АВ — ВС < 0. Но если знак ВD неизвестен (что бывает вообще тогда, когда B и D содержат неизвестные), то мы не можем умножать обе части неравенства на ВD. Тогда рассуждаем так: чтобы дробь была положительна, необходимо и достаточно, чтобы у нее числитель и знаменатель были одновременно или положительны, или отрицательны. Следовательно, неравенство (2) удовлетворится при таких значениях букв, при которых,
Таким образом, решение неравенства (1) сводится к решению системы двух неравенств, не содержащих знаменателей. 409. Доказательство неравенства. Нельзя установить каких-либо общих правил для обнаружения верности предложенного неравенства. Заметим только, что один из приемов состоит в том, что предложенное неравенство преобразовывают в другое, очевидное, и затем, исходя из этого очевидного неравенства, путем логических рассуждений доходят до предложенного. Приведем некоторые примеры. I. Доказать, что среднее арифметическое двух неравных положительных чисел больше их среднего геометрического, т. е. что
если а и b положительные числа, неравные друг другу. Предположим, что доказываемое неравенство верно. В таком случае будут верны и следующие неравенства:
Очевидно, что последнее неравенство верно для всяких неравных значений а и b, как положительных, так и отрицательных. Из этого, однако, нельзя еще сразу заключить, что и доказываемое неравенство верно; надо еще убедиться, что из последнего неравенства можно получить, как следствия, все предыдущие. Просматривая эти неравенства от последнего к первому, видим, что все они равносильны друг другу, если добавить ограничение, что буквы а
и b должны теперь означать только положительные числа, так как если одна из этих букв — отрицательное число, то √ab будет мнимое число, а если обе буквы — отрицательные числа, то Если допустим, что а = b, то тогда в написанных выше.неравенствах знак > изменится на знак = и мы придем к заключению, что среднее арифметическое двух равных положительных чисел равно их среднему геометрическому. II. Доказать, что величина дроби
заключается между большею и меньшею из дробей:
если все знаменатели b1 , b2 ...— числа положительные или все отрицательные. Пусть
Отсюда, если числа b1 , b2 ... bn положительные:
Сложив почленно все неравенства 1-й строки между собою и все неравенства 2-й строки между собою, получим: a1 + a2+ a3+ ... +an > ( b1 + b2+ b3+ ... +bn) q1 и a1 + a2+ a3+ ... +an < ( b1 + b2+ b3+ ... +bn) qn Разделив обе части этих неравенств на положительное число b1 + b2+ b3+ ... +bn окончательно найдем:
что и требовалось доказать. Так же доказывается предложение для того случая, когда все знаменатели числа отрицательные. III. Доказать, что если сумма переменных чисел х и у остается постоянной, то их произведение будет наибольшее при равенстве этих чисел. Пусть х + у = а, где а постоянное число. Если х = у, то каждое из этих чисел будет a/2 и тогда ху сделается равным Требуется доказать, что если х =/= у, то ху <
При неравных х и у последнее неравенство, очевидно, верно. Переходя от него последовательно к предыдущим неравенствам, замечаем, что все они равносильны. Значит, и первое неравенство верно. Если, напр., х + у =10, то наибольшая величина произведения есть 5•5 = 25. Понятие о комплексных числах. 410. Цель введения в алгебру мнимых чисел. Корень четной степени из отрицательного числа, как мы видели (ч. I, отдел 6 глава 6 § 167), не может быть выражен ни положительным, ни отрицательным числом; такой корень называется мнимым числом. Введение в алгебру мнимых чисел вызвано соображениями, подобными тем, по которым в нее допущены отрицательные числа: и те, и другие имеют целью обобщить некоторые алгебраические предложения и формулы. Напр., допустив мнимые числа, мы можем принимать, что квадратное уравнение имеет всегда два корня, что трехчлен 2-й степени разлагается всегда на два множителя первой степени, и т. п. Особенно важное значение имеют мнимые числа в теории уравнений высших степеней. Заметим, что корень всякой четной степени из отрицательного числа сводится к нахождению корня из квадратного корня из отрицательного числа; Поэтому в дальнейшем изложении мы будем говорить только о квадратном корне из отрицательного числа. 411. Условия, под которыми вводят мнимые числа. Этих условий два: 1) согласились рассматривать √— a , где — а есть какое угодно отрицательное число, как число особого рода, квадрат которого равен — а; 2) согласились производить над мнимыми числами действия и преобразования по тем же правилам, по каким они производятся над числами вещественными, принимая всегда, что ( √— a ) 2 = — а 412. Приведение √— a к виду √a √— 1. Мнимое число вида √— a можно заменить другим: √a √— 1. Действительно, √— a, согласно первому условию, есть такое число, квадрат которого равен — а. Но √a √— 1 также есть такое число, квадрат которого равен — а, потому что, применяя к этому выражению правило о возвышении в степень произведения (согласно второму условию), получим: ( √a √— 1) 2 =( √a ) 2 ( √— 1 ) 2 = а (—1) = — а. Условились сокращенно обозначать выражение √— 1 одною буквою i (начальная буква слова imaginaire, что значит мнимый). Таким образом, пишут: √— 4 = √4 √— 1 = 2i ; √— 3 = √3 √— 1 = i√3 Приведение мнимого числа к виду, содержащему множителя i, яснее обозначает мнимость радикала, которая без того может быть не вполне явною. 413. Комплексные числа. Общий вид всякого вещественного или мнимого числа есть a + bi, где а и b суть какие-либо вещественные числа, положительные или отрицательные, a i — обозначение √— 1. Число вида a + bi называется комплексным числом 3); в нем а есть вещественная часть, bi мнимая часть. При а = 0 оно обращается в чисто мнимое число bi = b√— 1 = √— b2; при b = 0 оно дает а + 0 • i, что равно одному вещественному числу а, так как произведение 0 • i, согласно условию второму § 411, должно приниматься равным нулю. Два комплексных числа вида a + bi, a — bi называются сопряженными. Под таким видом представляются корни квадратного уравнения, когда они мнимые. Два комплексные числа вида a + bi, —a — bi называются противоположными. 414. Основное начало, которому должны быть подчинены комплексные числа. Условившись над комплексными числами производить действия и преобразования по правилам, выведенным для вещественных чисел, при условии, что i2= — 1, мы должны будем подчинить комплексные числа следующему началу: Для того, чтобы комплексное число a + bi равнялось нулю, необходимо и достаточно, чтобы а = 0 и b = 0. Хотя предложение это можно было бы рассматривать как условие, которое мы ставим относительно комплексного числа и которое, следовательно, не нуждается в доказательстве, однако полезно обнаружить, что оно не находится в противоречии с поставленными нами ранее двумя условиями, а составляет естественное следствие их. Действительно, если положим, что a + bi = 0, тогда, совершая над этим равенством преобразования, дозволительные для равенств с вещественными числами, и принимая i2= — 1, мы будем иметь: a =— bi; a2 = (— bi)2 = b2i2 = — b2; a2 + b2 = 0. Так как a2 и b2 суть числа положительные, а сумма двух положительных чисел не может равняться нулю, то выведенное равенство возможно только тогда, когда каждое из них отдельно равно нулю; значит, необходимо: а = 0 и b = 0. Обратно, если положим, что а = 0 и b = 0, то a + bi = 0 + 0•i; принимая умножение на нуль и сложение с нулем в том же условном смысле, какой принят для вещественных чисел, мы должны принять, что 0 + 0•i = 0. Следствие. Для того чтобы числа a + bi и a' + b'i были равны, необходимо и достаточно, чтобы а =а' и b = b'. Действительно, если a + bi = a' + b'i, то (а — а') + (b — b') i = 0 и, Обратно, если а =а' и b = b', то число a + bi мы должны принимать равным числу a' + b'i, так как эти комплексные выражения в этом случае ничем друг от друга не отличаются. Из равенства комплексных чисел непосредственно следует, что если 2 числа равны одному и тому же 3-му, то они равны и между собою. Замечание. Относительно компексных чисел не принято никакого соглашения, какое из них считать большим другого. 415. Действия над комплексными числами. Чтобы произвести какое-нибудь действие над мнимыми числами, надо прежде всего каждое из них привести к виду комплексного числа a + bi, затем произвести действия над двучленами такого вида по тем правилам, которые выведены были для двучленов с вещественными членами (согласно условию второму § 411) и, наконец, в результате заменить везде i2 через — 1 (согласно условию первому того же §). Сложение, (a + bi) + (a1 + b1i) = (a + a1) + (b + b1)i (a + bi) + (a1 + b1i) + (a2 + b2i)= (a + a1+ a2) + (b + b1+ b2)i и т. п. Отсюда легко усмотреть, что сумма комплексных чисел обладает теми же свойствами, какие принадлежат сумме вещественных чисел, т. е. свойствами переместительным и сочетательным. Вычитание. (a + bi) — (a1 + b1i) = (a — a1) + (b — b1)i Отсюда видно, что к вычитанию комплексных чисел можно применять общее правило вычитания алгебраических чисел (ч. I, отдел 1 глава 3§ 22), т. е., чтобы вычесть какое-нибудь число, достаточно прибавить число противоположное; так, вместо того, чтобы от a + bi вычесть a1 + b1i, можно к a + bi прибавить — a1 — b1i. Заметим, что сумма или разность двух комплексных чисел может иногда оказаться числом вещественным (напр., сумма сопряженных комплексных чисел). Умножение. (a + bi) (a1 + b1i) = aa1 + a1bi +ab1i + bb1i2 = (aa1 — bb1) + (a1b + ab1)i Подобным образом можно составить произведение трех и более комплексных чисел. Легко убедиться (поверкой), что произведение комплексных чисел так же, как и вещественных (ч. I, отдел 1 глава 3 § 34), обладает свойствами: переместительным, сочетательным и распределительным (относительно сложения). Напр., чтобы проверить последнее свойство, выражаемое равенством: [(a + bi) + (a1 + b1i)] (a2 + b2i) = (a + bi)(a2 + b2i) +(a1 + b1i)(a2 + b2i) выполним действия, указанные в каждой части этого равенства. Левая часть дает: [(a + a1) + ( b+ b1)i] (a2 + b2i) = (a + a1) a2 + ( b+ b1)a2 i +(a + a1)b2i + ( b+ b1)b2 i2 = В правой части получается то же самое выражение. Проверим еще следующее важное свойство произведения: для того, чтобы произведение комплексных чисел равнялось нулю, необходимо и достаточно, чтобы одно из этих чисел равнялось нулю. Действительно, если (a + bi) (a1 + b1i) = 0, то (aa1 — bb1) + (a1b + ab1)i = 0 и следовательно,
Умножив первое уравнение этой системы на а и второе на b, сложим их: a2a1 + b2a1 = 0, или a1 (a2 + b2) = 0. (2) Умножив первое уравнение системы (1) на b и второе на а, вычтем из второго первое: a2b1 + b2b1 = 0, или b1 (a2 + b2) = 0. (3) Из равенств (2) и (3) заключаем, что или a2 + b2 = 0, или a1 = 0, b1 = 0. Если первое, то а = 0 и b = 0 и, следовательно, a + bi = 0; если второе, то a1 + b1i = 0. Обратно, пусть a + bi = 0, т. е. а = 0 и b = 0; но тогда и aa1 — bb1 = 0, и a1b + ab1 = 0; следовательно, и произведение (a + bi) на (a1 + b1i) равно 0 . Заметим, что произведение двух cопряженных комплекcных чисел (a + bi) (a1— b1i) равно положительному вещественному числу a2 + b2 . Деление. Обозначим частное (a + bi) : (a1+ b1i) через x + yi , где x и у предположим вещественными числами. Тогда, по определению деления, будем иметь: (a1+ b1i) (x + yi) = a + bi т. е. (a1x — b1y)+ (b1x + a1y)i = a + bi, откуда Умножив первое уравнение на a1 а второе на b1 и сложив оба уравнения, получим:
Умножив первое уравнение на b1 а второе на a1 и вычтя из второго первое, получим:
Формулы, найденные для х и у, дают возможное решение, если только a12 + b12=/= 0, т. е. если a1 и b1 не равны одновременно нулю; другими словами, если делитель В этом случае, следовательно, будем иметь:
Замечание. Это же частное мы могли бы получить проще, умножив в дроби
Возвышение в степень. Предварительно найдем результаты от возвышения в степень мнимого числа i, зная, что, согласно условию, i2 должно принимать равным — 1. i1 = i; Таким образом, последовательные степени i дают повторяющиеся результаты, а именно, следующие четыре: i, —1, — i, + 1. Чтобы узнать, какой из этих результатов получится при возвышении i в степень с показателем n, достаточно разделить п на 4 и обратить внимание только на остаток от деления. Так: i27 = i4•6 +3= i3 = — i Заметим еще, что i0 мы будем принимать равным 1. Теперь легко найдем результаты возвышения a + bi в степень с целым положительным показателем, так: (a + bi)2 = a2 + 2abi + b2i2 = (a2 — b2) + 2abi. и т. д. Извлечение квадратного корня. Положим, что √a+ bi = x + yi . Откуда: a + bi = (х2 — y2) + 2xyi. Следовательно, Вопрос приводится к нахождению вещественных корней этой системы. Возвысив оба уравнения в квадрат и затем сложив их, получим: (х2 + y2)2 = a2 + b2 и х2 + y2 = √a2 + b2 (Знак перед радикалом отброшен, так как при вещественных значениях х и у выражение х2 + y2 не может быть отрицательным.) Возьмем последнее уравнение совместно с первым уравнением системы (1); складывая их и вычитая, получим:
Из второго уравнения системы (1) усматриваем, что знаки у х и у должны быть одинаковые, если b > 0, и разные, если b < 0. Поэтому:
Замечание. Чтобы из комплексных чисел можно было извлечь корень третьей или высшей степени, им надо придать иной вид (тригонометрический), о чем мы здесь говорить не будем. Глава восьмая. Некоторые замечания об алгебраических уравнениях. Двухчленное уравнение. 416. Общий вид алгебраического уравнения. Мы видели (ч. I, отдел 4 глава 1 § 124), что уравнение, содержащее неизвестное в знаменателях, может быть приведено к целому виду. Далее мы знаем (ч. I отдел 9 глава 4 § 234), что уравнение, содержащее неизвестное под знаком радикала, может быть приведено к рациональному виду. Вследствие этого можем сказать, что всякое уравнение, в котором неизвестное связано с данными числами посредством конечного числа 6 алгебраических действий (сложения, вычитания, умножения, деления, возвышения в степень и извлечения корня (В предположении, что при возвышении в степень и при извлечении корня неизвестное не входит ни в показатель степени, ни в показатель корня.), может быть приведено к такому целому и рациональному виду: Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L = 0, где коэффициенты А, В, С. ..K и L суть постоянные вещественные или комплексные числа, а m есть показатель степени уравнения. Некоторые коэффиценты в частных случаях могут равняться 0. Уравнение такого вида называется алгебраическим. Алгебраические уравнения степени выше 2-й называются уравнениями высших степеней. 417. Некоторые свойства алгебраического уравнения. Уравнения высших степеней составляют предмет высшей алгебры. Элементарная же рассматривает только некоторые частные случаи этих уравнений. Высшая алгебра устанавливает следующую важную истину: всякое алгебраическое уравнение с вещественными коэффициентами имеет вещественный или комплексный корень (Теорема Г а у с с а) (1799). Допустив эту истину (доказательство которой в элементарной алгебре было бы затруднительно), не трудно показать, что алгебраическое уравнение имеет столько корней, вещественных или комплексных, сколько единиц в показателе его степени. Действительно, согласно теореме Гаусса, уравнение: Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L = 0 (1) имеет вещественный или комплексный корень; пусть этот корень будет а. Тогда многочлен, стоящий в левой части уравнения (1), должен делиться на х — α(§ 392). Если сделаем деление, то в частном получим многочлен степени m—1, у которого первый коэффициент будет А. Обозначив другие его коэффициенты соответственно буквами: (х — α) (Ахm-1 + В1хm - 2 + C1хm - 3 + ... + K1) = 0. (2) Приравняв нулю многочлен, стоящий во вторых скобках, получим новое уравнение, которое, по той же теореме, должно иметь некоторый корень β; вследствие этого левая его часть может быть разложена на два множителя: х — β и многочлен степени m — 2, у которого первый коэффициент попрежнему будет А. Поэтому уравнение (1) можно переписать так: (х — α)(х — β)(Ахm-2 + В2хm - 3 + ...) = 0. (3) Продолжая эти расоуждения далее, дойдем, наконец, до того, что многочлен, заключенный в последних скобках, будет 2-й степени, причем первый его коэффициент останется А. Разложив этот трехчлен на множителей (ч. I, отдел 9 глава 2 § 222), приведем уравнение (1) окончательно к виду: А(х — α)(х — β)(х — γ)...(х — λ) = 0, (4) где всех разностей: х — α , х — β... будет m. Очевидно, что уравнение (4) обращается в тождество при каждом из значений: х = α, х = β, х = γ,..., х = λ и не удовлетворяется никакими иными значениями х (если А=/= 0); значит, уравнение (1) имеет m корней α, β, γ... λ . В частных случаях некоторые и даже все корни могут оказаться одинаковыми. Полезно заметить еще следующие истины, доказываемые в высшей алгебре. Сумма корней всякого алгебраического уравнения Ахm + Bхm - 1 + Cхm - 2 + ... + Kх + L = 0 равна — B/A, а произведение корней равно L/A (примером может cлужить квадратное уравнение). Если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то число этих корней четное (примером может служить биквадратное уравнение). Если алгебраическое уравнение с вещественными коэффициентами имеет n корней вида p — qi, оно имеет n корней вида p — qi (примером может служить биквадратное уравнение, комплексные корни которого всегда сопряженные), и так как [x — (p + qi)][x — (p — qi)] = [(x — p) — qi][(x — p)+ qi] = то левая часть уравнения содержит в этом случае n вещественных множителей вида ax2 + bx + c. Алгебраическое уравнение нечетной степени с вещественными коэффициентами имеет, по крайней мере, один вещественный корень. Уравнения с произвольными буквенными коэффициентами степени не выше 4-й разрешены алгебраически, т. е. для корней этих уравнений найдены общие формулы, составленные из коэффициентов уравнения посредством алгебраических действий. В этом смысле уравнения с произвольными буквенными коэффициентами степени выше 4-й не могут быть разрешены алгебраически (теорема Абеля4)); однако, когда коэффициенты уравнений какой-угодно степени выражены числами, всегда есть возможность вычислить с желаемой степенью приближения все его корни как вещественные, так и мнимые. Указание способов такого вычисления составляет важную часть предмета высшей алгебры. 418. Двучленное уравнение. Двучленным уравнением называется уравнение вида: axm + b = 0, или, что то же самое, вида xm + b/a = 0 5). Обозначив абсолютную величину дроби b/a через q, мы можем двучленное уравнение написать: или xm + q = 0, или xm — q = 0. При помощи вспомогательного неизвестного эти уравнения всегда можно упростить так, что свободный член у первого обратится в +1, а у второго в —1. Действительно положим, что х = у m√q где, m√q есть арифметический корень m-й степени из q :тогда x m = q у m, уравнения примут вид: q у m + q = 0, т. е. q( у m +1) = 0; откуда: у m + 1 = 0; или Итак, решение двучленных уравнений приводится к решению уравнений вида 419. Решение двучленных уравнений третьей степени. Эти уравнения следующие: х3 —1 = 0 и х3 + 1 = 0. Заметив, что (§ 395): х3 —1 = х3—13 = (х—1) (х2+ x +1) и мы можем предложенные уравнения написать так: (х—1) (х2+ x +1) = 0 и (х + 1) (х2— x +1) = 0. Значит, первое из них имеет корни уравнений: (х—1) = 0 и (х2+ x +1) = 0, а второе — корни уравнений: (х + 1) = 0 и (х2— x +1) = 0. Решив их, находим, что уравнение х3 —1 = 0 имеет следующие три корня:
из которых один вещественный, а два мнимых; уравнение х3 + 1 = 0 имеет три корня:
из которых также один вещественный, а два мнимых. 420. Различные значения корня (радикала). Решение двучленных уравнений m-й степени имеет тесную связь с нахождением всех значений корня той же степени из данного числа. В самом деле, если буквою х обозначим какое угодно значение m√A , то, согласно определению корня, мы
будем иметь: x m = А Докажем, напр., что кубичный корень из всякого числа имеет три различных значения. Найти все значения 3√A значит, другими словами, решить уравнение x3 — А = 0. Обозначив арифметическое значение 3√A через q (оно может быть только одно, ч. I, отдел 6 глава 6 § 166), введем вспомогательное неизвестное y, связанное с х таким равенством: x = qy. Тогда уравнение x3 — А = 0 представится так: q3y3 — А = 0; но q3 = A; поэтому q3y3 — А = А (y3 — 1); следовательно, уравнение окончательно примет вид: y3 — 1 = 0. Мы видели, что это уравнение имеет три корня:
Каждое из этих значений, удовлетворяя уравнению y3 = 1, представляет собою кубичный корень из 1. Так как x = qy, то
Это и будут три значения 3√A; одно из них вещественное, а два мнимые. Все они получатся, если арифметическое значение кубичного корня из A умножим на каждое из трех значений кубичного корня из 1. Напр., кубичный корень из 8, арифметическое значение которого есть 2, имеет следующие три значения:
Замечание. В высшей алгебре доказывается, что двучленное уравнение x m — А = 0 имеет m различных корней; вследствии этого m√A имеет m различных значений, причем, если m число четное и А отрицательное, то все эти значения мнимые; если m четное и А положительное, то два значения вещественные (из них одно положительное, другое отрицательное, с одинаковой абсолютной величиной); наконец, если m нечетное число, то из всех значении А только одно вещественное.
|
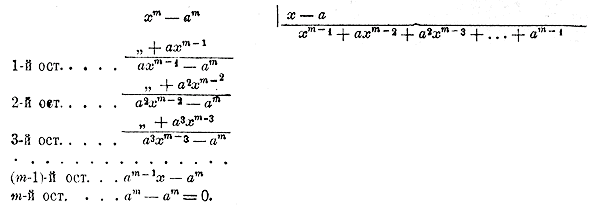
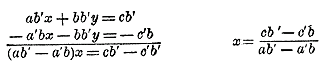
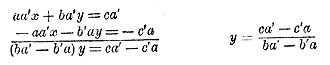

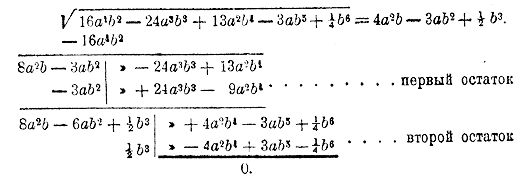
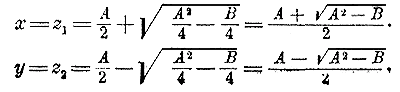
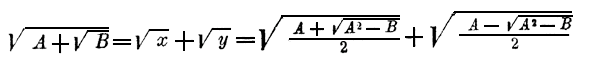
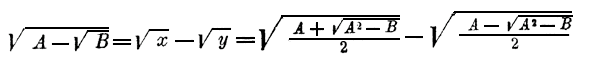
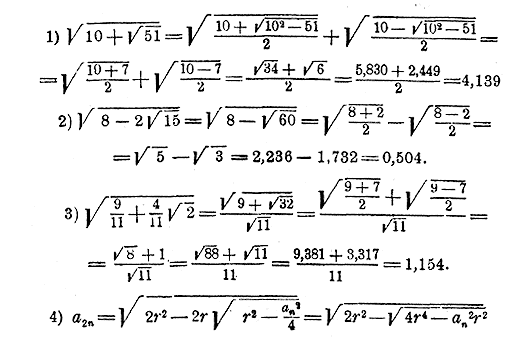
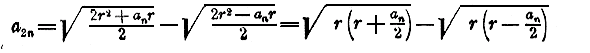
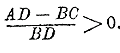 (2)
(2)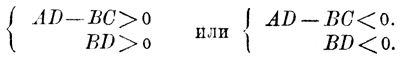
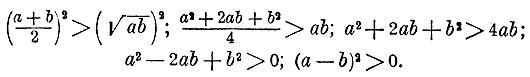
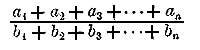
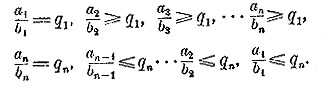

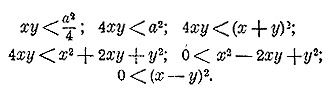
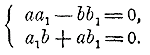 (1)
(1)
 (1)
(1)