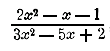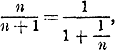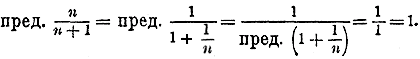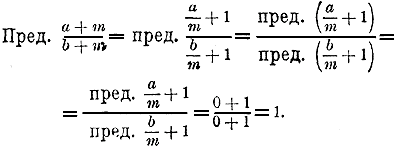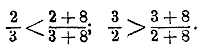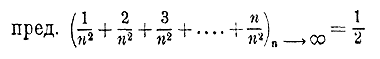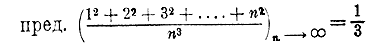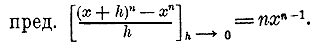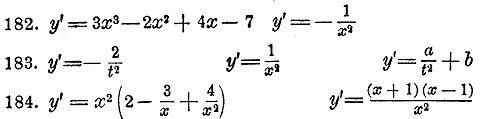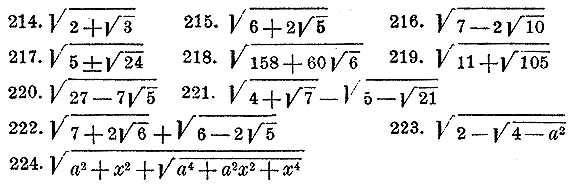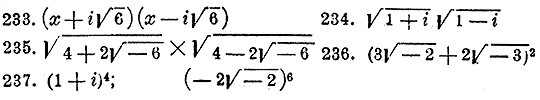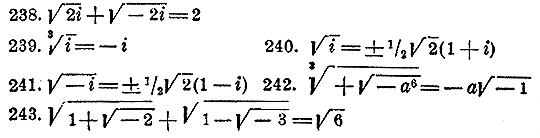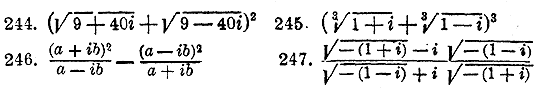| АЛГЕБРА В НАЧАЛО | ||
|
ОТДЕЛ ДЕВЯТНАДЦАТЫЙ. ЗАДАЧИ И УПРАЖНЕНИЯ. (В скобках поставлены соответствующие параграфы.) Основные сведения о пределах.
(Отдел 14 §§ 307-318.) 1. Найти предел, к которому стремится дробь
если х—>1. Решение. Если х—>1, то числитель и знаменатель данной дроби стремятся к 0. Но так как 0/0 есть неопределенное выражение, то мы остаемся в неизвестности, к какому пределу стремится данная дробь (и даже стремится ли она к какому бы то ни было пределу), если х—>1. Поступим так: предположим, что х равен не 1, а какому-нибудь переменному числу, приближающемуся к 1. Например, пусть x = l + h, где h какое-нибудь положительное число, стремящееся к нулю. Тогда величина данной дроби будет:
(сократить дробь на h мы имеем право, так как h =/=0). Предположим теперь, что h—>0 и, следовательно, х—>1
Тот же самый предел мы найдем, если допустим, что x = 1— h где h какое-нибудь положительное число, стремящееся к 0. Таким образом, будет ли х приближаться к 1, оставаясь больше 1 или оставаясь меньше 1, предел данной дроби будет один и тот же, именно 3. 2. Найти предел, к которому стремится дробь
если х—>1. 3. То же, если х—>0 4. Найти пред. 5. Найти пред. 6. Найти пред. Решение. Так как
то 7. Найти пред. 8. Найти пред. 9. Найти предел, к которому стремится дробь, если к числителю и знаменателю ее будем прикладывать одно и то же число, неограниченно возрастающее; другими словами, найти
Решение.
Таким образом, будет ли дробь a/b правильная (а< b), или неправильная (а>b), предел дроби, когда m—> ∞, оказывается один и тот же, именно 1. Отсюда следует, что правильная дробь, приближаясь к 1, увеличивается, а неправильная уменьшается. Таким образом, например.
10. Доказать, что если x >1, то пред. (хn )n —> ∞ = ∞ если x < 1, то этот предел есть 0 (показатель n предполагается целым положительным). Решение. Если х > 1, то можно принять, что х = 1 + h где h какое-нибудь положительное число. Тогда
Отсюда следует, что при h положительном хn = ( 1 + h )n > 1 + nh При безграничном возрастании n произведение nh, а поэтому и сумма 1 + nh, возрастает неограниченно; значит, пред. (хn )n —> ∞ = ∞. Пусть теперь x<1. Положим тогда, что
Ho x1 >1; поэтому по доказанному выше пред. x1n = ∞ и, следовательно, пред. ( x1n ) = 1/∞ = ∞ Отсюда, между прочим, вытекают те два предложения о бесконечных геометрических прогрессиях, которые были нами ранее доказаны другим путем (ч. I, отдел 10 глава 3 §§ 251,б и 251,в), а именно, что член aqn прогрессии при неограниченном возрастании n (т. е. при удалении от начала прогрессии) безгранично возрастает, если прогрессия возрастающая (q>1), и безгранично убывает (стремится к нулю), если прогрессия убывающая (q<1). 11. Доказать, что
12. Доказать, что 13. Доказать, что
14. Доказать, что
(n целое положительное число). 15. Найти 16. Построить график функции y = x + 1/x Найти предельное значение этой функции, если х —> 0, оставаясь положительным, и предельное значение, если х —> 0, оставаясь отрицательным. (отдел 15 §§ 319-333.) 17. Начертить график функции у = х2 — 3х + 2; определить подъем кривой при х = 1; х = 2; х = 3; вообще при х = х . 18. То же для у = 3х2 — 2х + 5. Найти производные от функций: 19. у = 5х у = — 71/2 х. 20. у = 3х— 4 у = 3 — 2х. 21. у = 10х2 у = — 0,8 х2 . 22. у = 3х2 — 2х + 4 у = х2 — 2х — 1. Возрастание или убывание функций. Maximum и minimum. (отдел 15 §§ 334-335.) 23. Построить график функции у = 1/4( 3х2 — 4х — 7) между х = — 3 и х = 2. Определить (и проверить на чертеже), при каких значениях х функция возрастает и при каких убывает. Имеет ли функция minimum или maximum и чему он равен? 24. Проследить изменение функции: у = 7х2 + 3х — 2, т. е. определить, при каких значениях х функция возрастает при каких убывает и имеет ли maximum, или minimum и какие. То же для функций: 25. у = — х2 + 8х + 1 у = — 5х2 + 4х + 1 26. у = 1/2 х2 + 3х — 7 у = 0,1х2 — 1/4 х + 2 27. у = х2 + 3 у = — х2 + 7 28 у = х2 — 4х у = х2 + 4х 29. у = 2х2 — 8х + 5 у = — 3х2 + 9х — 9 30. у = 2 — 3х — х2 у = 7 + 2х — 3х2 31. у = (х —3)2+(3х —5)2 32. у = √х2 — 2х +10 у = √3 — 4х—3х2 Указание. Если радикал рассматривается только в положительном значении, то очевидно, что в двух последних примерах y изменяется в том же смысле, в каком изменяется подкоренная величина. Поэтому вопрос приводится к рассмотрению изменения трехчленов х2 — 2х +10 и 3 — 4х—3х2 Maximum и minimum. (отдел 15§§ 334-335.) 33 Данное число а разделить на такие две части, чтобы произведение их было наибольшее из всех возможных. Решение. Пусть одна часть, х, тогда другая часть равна а — х и их произведение будет х (а — х) = ах — х2 . Производная этого двучлена есть а — 2х. Из признаков возрастания и убывания функций (§ 335) следует, что если а — 2х > 0, т. е. х < 1/2 a , то функция возрастает; если а — 2х < 0, т. е. х > 1/2 a , то функция убывает. Чиячит при х = 1/2 a наша функция получает maximum. Тогда другая часть будет равна .-a — 1/2 a = 1/2 a, т. е. обе части окажутся одинаковы. Мы приходим таким образом к следующему выводу, который полезно заметить: если сумма двух переменных чисел равна постоянному числу, то их произведение будет наибольшее из всех возможных тогда, когда эти числа сделаются равными между собою. Например, если х + у = 10, то произведение ху будет наибольшее, когда х = у = 5. Выводом этим приходится иногда пользоваться для решения различных задач на maximum. Приведем этому примеры. 34. Из всех прямоугольников с данным периметром какой будет иметь наибольшую площадь? Решение. Пусть данный периметр есть 2р, основание х и высота у. Тогда площадь равна ху. Так как х + у есть полупериметр, равный постоянному числу р, то maximum произведения ху будет при х = у, т. е. тогда, когда прямоугольник сделается квадратом. 35. В круге данного радиуса r вписать прямоугольник о наибольшею площадью. Решение. Если х и у будут основание и высота вписанного прямоугольника, 36. В данный треугольник вписать прямоугольник с наибольшею площадью так, чтобы его основание лежало на основании треугольника, а две вершины упирались в боковые стороны его. Решение. Обозначим основание и высоту треугольника b и h и прямоугольника х и у. Из подобия треугольников находим: x : b = (h — y) : h; откуда: площадь прямоугольника Требуется найти, при каком значении у эта дробь будет иметь наибольшее значение. Но в этой дроби знаменатель и множитель b в числителе суть числа постоянные; поэтому дробь получит наибольшее вначение тогда, когда произведение (h— y)y сделается наибольшим. Но в этом произведении сумма сомножителей h — у и у есть число постоянное; вследствие этого maximum
произведения (h— y)y будет при (h— y) = y, 37. Из всех прямоугольников, вписанных в круг данного радиуса r, какой имеет наибольший периметр? Решение. Вопрос приводится к нахождению maximum суммы х + √4r2 — х2. Вместо этой суммы нам выгоднее искать maximum ее квадрата: (х + √4r 2 — х2)2 = х2 + 4r 2 — х2 + 2х √4r 2 — х2 = 4r 2 + 2х √4r 2 — х2 и, следовательно, maximum произведения х√4r 2 — х2. Квадрат этого произведения, равный х2(4r 2 — х2), имеет maximum при х2 = 4r 2 — х2, так как сумма сомножителей есть число постоянное (4r 2). Значит, х = r √2 , но тогда и высота прямоугольника будет равна √4r 2 — х2 = √4r 2 — 2r 2 = r √2 т. е. прямоугольник будет квадратом. 38. В треугольнике даны оcнование (а) и сумма (s) его боковых сторон. Каковы должны быть эти стороны, чтобы площадь треугольника была наибольшая? Решение. Если х и у будут боковые стороны треугольника, то периметр его равен Δ = √p(p—a)(p—x)(p—y) и искать maximum произведения (р — х) (р — у). 39. Какой из всех прямоугольников с данною диагональю имеет: 1) наибольшую площадь; 2) наибольший периметр? 40. В круге данного радиуса r проведена хорда. Какова должна быть эта хорда, чтобы треугольник, образованный ею и двумя радиусами, проведенными к концам хорды, имел наибольшую площадь? Указание. Обозначив длину хорды 2х, мы приведем вопрос к нахождению maximum выражения х√r 2 — х2, или его квадрата х2(r 2 — х2). В окончательном результате увидим, что хорда должна быть стороною вписанного квадрата. 41. Какой из всех прямоугольников с данным периметром 2р имеет наименьшую диагональ? Указание. Если стороны прямоугольника будут х и у, то диагональ его выразится Скорость как производная от пространства. (отдел 15 §§ 337-341.) 42. Некоторое тело движется прямолинейно, таким образом, что в конце t-й секунды от начала движения оно оказывается удаленным от своего начального положения на расстояние е, определяемое равенством: е = 4 — 3t + t2. Определить: а) закон скорости этого движения; б) когда скорость положительна, когда она отрицательна и когда равна нулю; в) найти maximum удаления тела от начального положения. 43. Решить те же вопросы, если удаление в выражается формулой: e = 2t2 — 4t + 5. Ускорение как производная от скорости. (отдел 15§§ 342-343.) 44. Тело движется таким образом, что скорость v этого движения в зависимости от времени t (сек.) выражается формулой: v = 6t — 4t2. Определить: а) когда скорость возрастает; б) когда она убывает; в) maximum скорости; г) закон уcкорения. 45. Тело движется по прямой линии; его удаление е от некоторой определенной точки О. взятой на этой прямой, выражается в зависимости от времени t формулой: e = 3/2— 2t + 1/2 t2. Определить: а) расстояние тела до точки О в момент, от которого начинается счет времени (в момент t = 0); 46. Те же самые вопросы относительно движения тела, которого расстояние от точки O определяется формулой: е = 8 — 7 t + t2 47. Точка движется по прямой Ох таким образом, что ее расстояние е от О в конце 2-ой секунды выражается формулой: е = t2 — 12 t. Найти закон скорости и закон ускорения. Когда скорость сделается равной нулю? В какой момент будет minimum e ? 48. Скорость некоторого прямолинейного движения выражается формулой: (отдел 15 §§ 344—346.) Исследовать следующие функции 3-й степени и построить их графики: 49. у = х3 — 1/2х2 — 6х + 21/2 у = 1/3 х3 — х2 — 31/3 х + 8 50. у = х3 — 6х2 + 5х + 11 у = 3х3 — 3х2 — 5х + 2. 51. у = х3 + 2х2 — х — 1. 52. у = х3 — 7х — 4; 53. у = х3 — 13х + 12; 54. у = х3 — 7х + 5; 55. у = х2(6 — х). Замечание. Если значения данной функции настолько велики, что их неудобно изобразить на чертеже, то можно все их уменьшать в несколько раз. Например, при исследовании функции: у = х3 + 15х2 + 12 х — 27. удобнее уменьшить значения функции в 9 раз, т. е. взять функцию: 1/9 у = 1/9 х3 + 5/3 х2 + 4/3 х — 3. Графическое решение уравнения 3-й степени. (отдел 15§ 347.) Решить графически следующие уравнения: 56. х3 + х — 4 = 0. 57. х3 —3х = —2. 58. х3 —3х =1,5. 59. х3 —3х + 1 = 0. 60. х3 + х —7 = 0. 61. х3 —х — 1 = 0 62. х2 — 2/x = 1. 63. х2 — 2/x = 4. 64. Замечание. Последний пример можно свести к построению параболы 3-й степени (отдел 15§§ 348-349.) 66. Построить график у = 4/x между x = — 4 и x = + 4. Найти предельные значения при х = ± ∞ и x = 0. Найти производную от этой функции и при ее помощи определить, где функция возрастает и где убывает и куда направлена еe вогнутость. 67. Построить график у = — 1/x . Сравнить его с графиком у = 1/x (черт. 23)' 68. Построить графики функций: 1) у = x + 1/x 2) у = x — 1/x Найти производные этих функций и при их помощи решить вопросы о возрастании или убывании функций, а также о maximum и minimum их. Замечание. Графики указанных функций можно, конечно, cтроить, составив предварительно таблицы их значений для нескольких произвольно взятых значений х. Но можно поступить и так: построить (при одних и тех же осях и в одном и том же масштабе) график функции у = 1/x (это будет гипербола, изображенная на черт. 23) и график функции у = х (это будет биссектриса углов хОу и х'Оу'). Затем все ординаты биссектрисы увеличить (для функции у = x + 1/x или уменьшить (для функции у = x — 1/x) на соответствующие ординаты гиперболы. Этот прием можно употреблять вообще тогда, когда данная функция представляет собою сумму или разность двух других функций. 69. Построить графики х2 — 7 и 4/x. Найти точки пересечения и при их помощи определить корни уравнения х3 — 7х — 4 = 0 (т. е. уравнения х2 — 7 = 4/x). 70. Построить графики у = 1/x +1 и х2 + 2х между х = — 3 и х = 2. Найти точки пересечения и при их помощи решить уравнение х3 + 2х2 — х—1 = 0.
(отдел 16 §§ 350-352; повторить отдел 3 глава 3 §§ 115-117 части I). 71. Каково будет уравнение прямой, параллельной оси x-ов и отсекающей от оси у-ов отрезок, равный +2; +3 1/2; — 4; —10,5 ? 72. Каково будет уравнение прямой, параллельной оси у-ов и отсекающей от оси х-ов отрезок, равный +3; — 5; (вообще m)? 73. Какая прямая выражается уравнением: а) у = 0; б) x = 0? 74. Что можно сказать о прямой, выражаемой уравнением вида у = ах: а) если а > 0; б) если а < 0? 75. Какая прямая выражается уравнением: а) у = x б) у = — x ? 76. Чему равен угловой коэффициент прямой, выражаемой следующим уравнением: а) у = 2х + 5 б) у = х — 3 в) у = 1/2 х г) у = 7 — 3x д) у = — 0,5x е) у = — x 77. Чему равны угловой коэффициент и начальная ордината прямой, выражаемой уравнением: а) 3х + 2у = 10 б) — 0,7y + 3/4 х — 5 = 0 в) ах + bу = с ? 78. Каким уравнением выражается: а) ось x - ов; б) ось у-ов? 79. Если две прямые, выражаемые уравнениями вида: у = ах + b и у = а1х + b1 параллельны между собою, то что можно утверждать об угловых коэффициентах а и а1 ? 80. Найти угол, образуемый двумя пересекающимися прямыми у = ах + b и у = а1х + b1 .
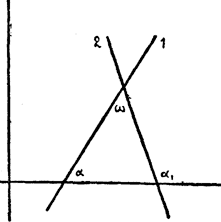
Черт.1 Решение. Из чертежа 1-го видно, что ω = α1 — α; следовательно,
Пусть, например, у = 2х — 3 и у = 5х + 1. Тогда
и log tg ω = log 3 — log 11 = 0,4771 — 1,0414 = 1,4357; ω = 15°15' (приблизительно). 81. Найти условие перпендикулярности двух прямых у = ах + b и у = а1х + b1 . Решение. Из предыдущей задачи видно, что если ω = 90°, то tg ω = ∞ и 1+ aа1= 0; следовательно, искомое условие есть следующее: а1 = — 1/a Наиримеp, прямые у = 2х — 3 и у = — 0,5х— 3 перпендикулярны, так как —0,5 = —1/2 82. Если прямая выражается уравнением:
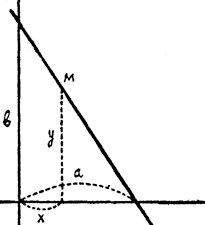
то что означают здесь a и b ? Решение. Положив в уравнении х = 0, найдем: у = b. Значит, на прямой находится точка (0,b), т. е. прямая отсекает, от оси у-ов отрезок, равный b. Равным образом, положив у = 0, найдем: х = а. Значит, прямая отсекает от оси x-ов отрезок, равный а. Это же можно видеть из чертежа 2-го.
Черт.2 Из подобия треугольников следует, что ординаты произвольной точки М прямой удовлетворяют пропорции: у: b = (a — х): а, откуда: ау = аb — bх ; bх + ау = аb. Разделив все члены на аb, найдем:
Составить уравнение прямой, проходящей через точку: 83. (2,5) (—2,5) (2,—5) ( — 2,—5) 84. (0,7) (0,—7) (3,0) (—3,0) Составить уравнение прямой, проходящей через следующие пары точек: 85. (1,5) и (2,3) (—3,2) и (7,—4). 86. (0,0) и (5,6) (0,4) и ( — 2,—3). 87. (0,7) и (2,0) (—2,—3) и (7,8). 88. Даны две точки: (2,5) и (7,3). Найти расстояние между ними. Найти расстояние между двумя точками каждой из следующих пар: 89. (—3,5) и (2,3) ( — 3,5) и (2,—3). 90. (3,—5) и (2,3) (3,—5) и (—2,—3). 91. Проверить, что если даны две точки: (x1 , y1) и (x2, y2), то при всех возможных случаях расположения этих точек расстояние l между ними выражается формулой:
(отдел 16 § 353.) 92. Написать уравнение окружности, центр которой совпадает с началом координат и радиус равен: а) 5; б)8/3; в) 2,7. Написать уравнение окружности, радиуса 10, центр которой лежит в точке: 93. 1) (12,13) 2) (10,13) 3) (10,10) 94. 1) (7,13) 2) (7,8) 3) (0,11) 95. 1) (0,5) 2) (12,0) 3) (3,0) 96. 1) (—2,4) 2) (—2,—3), 3) (7,—5) 97. Найти радиус окружности, выражаемой уравнением: а) х2 + y2= 100 б) х2 + y2 =50. Показать, что следующие уравнения выражают окружности, найти их радиусы (перед знаками квадратных радикалов надо подразумевать оба знака ±): 98. 25х2 + 25y2 = 289 4х2 + 4y2 = 49 99. у = √16 — х2 у = √36 — х2 . 100. у = √20 — х2 у = 1/3 √100 — 9х2 101. у = 1/2 √81 — 4х2 (x — 2)2 + (y — 1)2 = 25 102. (x + 31/3)2 + (y — 4)2 = 81/4 103. Показать, что уравнение 3х2 + 3y2 + 8х — 6y = 20 (у которого коэффициенты при х2 и y2 одинаковы и нет числа, содержащего ху) есть уравнение круга; определить его радиус и положение центра. Решение. Разделим все члены на общий коэффициент при х2 и y2 : х2 + y2 + 8/3х — 2y = 20/3 или х2 + 8/3 х + y2 — 2y = 20/3 Чтобы дополнить сумму первых 2 членов до полного квадрата, надо к ней добавить (4/3)2; чтобы сделать то же самое с суммой 3-го и 4-го членов надо добавить к ней 1х2. Добавим же к каждой части уравнения по (4/3)2 +1 , т. е. по 25/9; тогда получим: (х + 4/3)2 + (у —1)2 = 20/3 + 25/9 = 85/9. Отсюда видно, что уравнение представляет окружность, которой центр находится в точке (—4/3, 1) и радиус равен √ 85/9 = 1/3√ 85 104. Показать (таким же приемом, какой указан в решении предыдущей задачи), что вообще уравнение вида: Aх2 + Aх2 + Bx + Cy + D = 0, у которого коэффициенты при х2 и y2 одинаковы и нет члена с ху, выражает окружность; найти ее радиус и положение центра. Найти радиус и положение центра окружностей, выражаемых уравнениями: 105. х2 + y2 — 12х —16y + 24 = 0 106. х2 + y2 = 2у + 35 107. у = — 7 ±√16 — х2— 6x 108. х2 + y2 + 8х — 6y — 3 = 0 109. у = 3/2 ±1/2√20x — 4х2+11 110. 5х2 + 5y2 — 9y — 38 = 0 111. Вычислить (с точностью до 0,001) координаты точек, в которых прямая линия у = 2х — 3 пересекается с окружностью х2 + y2= 10 (отдел 16 §§ 357-361.) Показать, что следующие уравнения приводятся к виду 112. х2 + 4y2= 100 3х2 + 16y2= 192 113. 25х2 + 81y2= 2025 4х2 + 9y2= 144 114. 115. y = 1/2√36 — х2 y = 2/5√100 — х2 116. y = 3/8√64 — х2 y = 1/2√20— х2 Найти положение центра и величину и положение осей эллипсов, выражаемых следующими уравнениями:
Показать, что следующие уравнения приводятся к виду:
т. е. что они выражают эллипс, центр которого лежит в точке (m,n) и большая ось параллельна оси х-ов: 123. y = ± 4/5√10x — х2 124. y = 1 ± 1/4√108 —9 х2— 36 х 125. На эллипсе, заданном уравнением
взята точка, которая при положительной абсциссе имеет ординату 1. Составить уравнение касательной, проходящей через эту точку. Найти координаты точек пересечения этой касательной с осями координат. 126. То же, если точка взята на эллипсе: y = ± 1/5√ 25 — х2 и при положительной ординате имеет абсциссу 3. (отдел 16 §§ 363—368.) Показать, что следующие уравнения приводятся к виду 127. 9х2 — 4y2 = 36 128. у = 3/4√ х2— 16 129. у = 5/3√ х2— 9 130. у = 1/2√ х2— 64 131. у = √ х2— 16 132. у = 2/3√ х2— 81 Каковы будут величины осей у гипербол:
Определить положение центра и осей гипербол, данных уравнениями: Показать, что следующие уравнения приводятся к виду:
т. е. что они выражают гиперболу, центр которой лежит в точке (m,n) и оси параллельны координатным осям, вещественная ось параллельна оси x-ов, мнимая ось параллельна оси у-ов: 139. y = 1 ± 2/3√ х2— 6 х 140. y = — 3 ± 2/5√ х2+ 10 х 141. На гиперболе: 142. То же для гиперболы: у = ± 2/3√ х2— 49 , если взятая на ней точка при положительной ординате имеет абсциссу, равную 8. (отдел 16 §§ 370-375.) Определить положение вершины, оси и директрисы парабол, заданных следующими уравнениями: 143. y2= 10х 144. y2= 6х 145. y2= 9х 146. y = ±√3x 147. y = ±√7x 148. y = ±√12x (В этих шести случаях ось параболы лежит на оси x-ов и направлена в положительном ее направлении.) 149. y2= —9х 150. y2= —10х; 151. y2= —х (В трех последних примерах ось направлена в отрицательном направлении оси x-ов.) 152. y2 = 8x — 16 153. y2 = 5x + 15 154. y = ±√2x + 8 (В последних трех примерах координаты вершины будут: (2,0), (—3,0) и (—4,0); ось идет по положительному направлению оси х - ов.) 155. (у + 2)2 = 4x; y = 1 ±√16x ; (у — 4)2 = 12x (Координаты вершины параболы: (0, — 2), (0,1) и (0,4). 156. 2 y2 + 2y — 11x + 73 = 0 Решение. Уравнение можно преобразовать так: y2 + y= 11/2 x — 73/2 (y+ 1/2)2 = 11/2 x — 73/2 + 1/4 (y+ 1/2)2= 11/2 x — 145/4; (y+ 1/2)2 = 11/2 (x — 290/44) Отсюда видно, что вершина лежит в точке (290/44,—1/2) ось параллельна оси х-ов и направлена в положительную сторону; параметр равен 11/4 = 23/4 157. y2 + 6y — 9x = 0 158. у = 1/2 x2 159. 15у = x2 160. — 8у = x2 Как мы видели в § 212 (ч. 1 отдел 9 глава 1), кривая, выраженная уравнением вида 161. у = 2х2 — 8 у = 3х2 + 6 у = 5х2 — 10 162. у = 3х2— 12 у = х2 — 25 у = 4х2+ 16 163. у = — 3х2 + 12 у = — 4х2 + 8 у = —2х2 —10 Приняв во внимание отдел 9 глава 2 § 224 и отдел 15 глава 4 § 335, определить координаты вершины параболы и направление ее оси, а также решить вопрос о возрастании или убывании функции и о ее нулевых значениях (т. е. точках, в которых парабола пересекается с осью x - ов): 164. у = х2 + 5х + 4 165. у = х2 + 11/6 х — 5/3 166. у = 8/3 — 2/3 х — х2 167. у = 2 + 4х — х2 168. у = х2 + 3/2 х — 9/2 169. у = — х2 + 4х — 5 170. у = 5 — 2х — х2 171. у = — х2 + 6х — 9 172. На параболе у = 3/2 х2 взята точка с абсциссой 2. Составить уравнение касательной, проведенной через эту точку. 173. То же для точки с абсциссой —2. 174. На параболе у = 1/3 х2 взяты две точки, у которых одна и та же ордината, именно —12; составить уравнения касательных, проведенных через эти точки. (отдел 17 §378.) Найти первообразные функции по следующим производным: 175. у' = а у' = — 5 у' = 1/5 у' = 2,3 176. у' = х у' = 3х у' = 1/3 х у' = 0,7x 177. у' = х + 2 у' = х —7 у' = 2х + 1/2 178. у' = 5х —2 у' = 2а ± b у' = mх ± р 179. у' = 5х2 у' = — 2х2 у' = nх2 ± m 180. у' = 3х2 + 1х у' = 12х2 — 4х у' = 21х2 + 8х — 2 181. у' = х2 у' = 4х3 — 7х у' = ax2 + bx + c
(в последних двух примерах надо предварительно раскрыть скобки). (отдел 17 § 377.) 185. Найти площадь, ограниченную прямой у = 2х + 1, осью x - ов и двумя ординатами, соответствующими абсциссам x = 4 и x = 25. Проверить полученное число посредством формулы элементарной геометрии для площади трапеции. 186. То же между x = 1 и x =10; между x =—1 и x =15. 187. Определить площадь, ограниченную параболой у = 2х2 + 3, осью x - ов и 2 ординатами при x =3 и x = 9. 188. То же между x = 0 и x = 8; между x = 1 и x = 10. 189. Определить площадь, ограниченную параболой у = 3 + 4x + 3х2, осью x - ов и ординатами, соответствующим абсциссам х =1 и х = 2. 190. Найти площадь, заключенную между осью x - ов и дугою параболы 191. Дана кривая 192. Определить площадь, ограниченную кривою, выраженного уравнением 193. Найти точку пересечения кривой По данному закону скорости найти закон пространства. (отдел 17 § 379.) Найти закон пространства, если: 194. v = 2 + 3t и е = 3, если t = 0 195. v = t2 + 4t — 5 и е = 4, если t = l 196. 197. 198. v = (t — 1)(t — 3) и е = 5, если t = 0 199. 200. Поезд движется между двумя последовательными остановками со скоростью 1) все расстояние между остановками поезд проходит в 2 минуты; 2) maximum скорости будет 1/2 км в минуту; и 3) расстояние между остановками равно 2/3 км. По данному закону ускорения найти закон скорости. (отдел 17 § 380.) 201. Камень брошен вертикально вниз со скоростью 30 м в секунду; ускорение от действия силы тяжести равно 9,8 м в секунду; найти скорость тела по прошествии t секунд от начала падения и пространство, которое камень пройдет в t секунд. 202. Тело движется по прямой линии с ускорением w = 3t2 + t — 2. Найти maximum и minimum скорости, если известно, что когда t =1, тогда v = 10. 203. Тело движется по прямой линии с ускорением w = 2 + 6t. Определить закон скорости, если известно, что v = — 2, если t = 0. (отдел 17 §§ 381—383.) 204. Парабола у2 = 4ах, которой ось расположена на оси х - ов (в положительном ее направлении), вращаясь вокруг этой оси, производит так называемый параболоид вращения. Найти объем, ограниченный поверхностью этого параболоида и плоскостью, перпендикулярною к оси х - ов в точке ее х = b. Показать, что этот объем равен 1/2 объема цилиндра, описанного около параболоида. 205. Взята часть гиперболы у = 1/x, лежащей в угле хОу, и из концов ее проведены перпендикуляры на ось х - ов; один из этих перпендикуляров оказался на расстоянии а от оси y-ов, другой на расстоянии b > а. Найти объем тела, происходящего от вращения вокруг оси х - ов фигуры, ограниченной этой осью, двумя указанными перпендикулярами и дугою гиперболы. Показать затем, что если b —> ∞, то этот объем приближается к конечному пределу. 206. Уравнение 207. Найти объем тела, производимого вращением вокруг оси х - ов кривой
(отдел 18 §§ 391—395.) 210. Найти остаток от деления многочлена х4 — 3х3 — 5х2 + 20 х — 8 на х — 1; 211. Определить численную величину а в многочлене: 212. Как можно быстро решить кубичное уравнение, если один его корень известен? Например, решить уравнение х3 — 6х2 + 11 х — 6 = 0, которого один корень есть 1. 213. Ученик запомнил, что делимость или неделимость двучленов хm — am и хm + am на двучлены х — a и х + a зависит от того, будет ли показатель m четное число или нечетное; но он забыл, когда делимость происходит при четном показателе и когда при нечетном. Как можно легко восстановить в памяти все эти 4 случая делимости? (отдел 18 § 403.) Преобразовать следующие сложные радикалы в сумму или разность двух простых радикалов:
225. Пусть аn означает длину стороны правильного n- угольника, вписанного в круг радиуса R. Тогда, как известно из геометрии:
Преобразовать эту формулу в разность двух простых радикалов. 226. Найти необходимое и достаточное условие, чтобы корни уравнения Дополнительные Сведения о неравенствах. (отдел 18 §§ 404 — 409.) 227. Показать, что при всяком вещественном значении х имеет место следующее неравенство:
228. Доказать, что если а и b два положительные числа и а > b, то √a —√b < √a — b. 229. Доказать, что если n > 0, то
230. Доказать, что если х и у два положительных неравных числа, то 4(х3 + y3 ) > (х + y)3 . 231. Умножение обеих частей неравенства F1(x) > F2(x) на f (x) приводит ли всегда к равносильному неравенству? Если, например, обе части неравенства: 2х — 3 > х + 7 умножим на 2 — х, то получим ли равносильное неравенство? (отдел 18 §§ 410-415.) 232. Проверить равенство: i7 + i18 + i25 + i35 + i97 + i100 = 0. Вычислить выражения:
Проверить возвышением в квадрат или в куб следующие равенства:
Выполнить указанные действия:
248. Найти необходимое и достаточное условие для того, чтобы произведение 249. То же для частного (a + bi):(c + di). 250. Все ли действия над комплексными числами, выраженными под видом a + bi, выполнимы? Упростить выражения:
255. Обозначив для краткости:
проверить равенства: 1) α13 = α23 = α33 = l; 2) α1 + α2 + α3 = 0; 3) α1α2 α3 =1; 4) α12 = α2 ; 5) α22 = α1; 6) l + α1 + α12 = 0. 256. Доказать при помощи комплексных чисел, что всякое число, равное какой-нибудь степени суммы двух квадратов, есть само сумма двух квадратов. Решение. (a2 + b2)m = [(a + bi )(a — bi)]m = (a + bi )m (a — bi)m Но если выполним, согласно биному Ньютона возвышение в степень, то найдем, что (a + bi )m = A + Вi и (a — bi)m = А — Вi, следовательно, (a2 + b2)m = (A + Вi) (А — Вi) = A2 + B2.
|